Седумаголник

Седумаголник – многуаголник со седум темиња и седум страни.

Правилен седумаголник
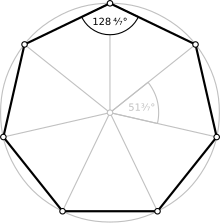Правилен седумаголник
Вид	правилен многуаголник
Рабови и темиња	7
Шлефлиев симбол	{7}
Коксетер–Динкинови дијаграми
Група на симетрија	диедарска (D7), ред 2×7
Внатрешен агол	≈128.571°
Својства	испакнат, впишан, рамностран, изогонален, изотоксален

Правилен седумаголник

Правилниот седумаголник е седумаголник кај кого сите страни се со еднакви должини и сите внатрешни агли се еднакви.

Внатрешните агли на правилен седумаголник имаат по 128,57° (степени), а збирот на сите внатрешни агли на кој било седумаголник изнесува 900°.

Ако основната страна на седумаголник е $t\,\!$, неговата плоштина се определува со формулата: $P={\frac {7t^{2}}{4}}\mathop {\mathrm {ctg} } \,{\frac {\pi }{7}}\approx 3{,}63391t^{2}$

Плоштината може да се пресмета и со: $P={\frac {7}{2}}R^{2}\sin {\frac {2\pi }{7}}=7r^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{7}}$ каде $R$ - е полупречник на опишаната кружница, а $r$ - е полупречник на впишаната кружница.

Периметарот на седумаголникот чија страна е со должина $t\,\!$ ќе биде еднаков на $7t\,\!$ односно $14R\sin {\frac {\pi }{7}}$ или $7r^{2}\mathop {\mathrm {tg} } {\frac {\pi }{7}}$.

Конструкција

Правилен седумаголник не може да се конструира со шестар и линијар. Во 1796 година Гаус докажал дека правилен n-аголник може да се конструира со помош на шестар и линијар само кога $n$ е прост број во облик $2^{p}+1$, каде $p=2^{k}$, за $k=0,1,2,...$. Како 7 е прост број кој го нема тој облик, конструкцијата на правилен седумаголник не е можна.

Конструкција на внатрешен агол во правилен седумаголник со помош на обележен линијар

Можно е да се изведе конструкција со помош на обележен шестар и линијар, но таа не се прифаќа како математички коректна.

Каде може да се види седумаголник

Некои монети кои денес се користат во Обединетото Кралство, како некои монети во Европската унија имаат изменет облик на правилен седумаголник затоа што таквите парички се со карактеристичен облик и лесно можат да се препознаваат на допир, а од друга страна имаат неочекувана особина, иако немаат кружен облик можат да се користат во апаратите кои работат со монети.

Поврзано

• Многуаголник
• Правилен многуаголник
• Четириаголник
• Петаголник
• Шестаголник
• Осумаголник
• Деветаголник
• Десетаголник

Надворешни врски

• Седумаголник на Mathworld
• Дефиниција и особини на седумаголник, со интерактивна анимација
• Неколку приближни конструкции на правилен седумаголник