Википедија

Релативна диелектрична константа

Релативна диелектрична константа на некои материјали на собна температура под честота од 1 kHz
Материјал εr
Вакуум 1 (по дефиниција)
Воздух 1,00058986 ± 0,00000050
(на собна температура, за 0,9 MHz),[1]
ПТФЕ/Тефлон 2,1
Полиетилен 2,25
Полиамид 3,4
Полипропилен 2,2–2,36
Полистирен 2,4–2,7
Јаглероден дисулфид 2,6
Мајлар 3,1[2]
Хартија 3,85
Електроактивни полимери 2–12
Лискун 3-6[2]
Силициум диоксид 3,9 [3]
Сафир 8,9–11,1 (анизотропна) [4]
Бетон 4,5
Пирекс (Стакло) 4,7 (3,7–10)
Неопрен 6,7[2]
Гума 7
Дијамант 5,5–10
Сол 3–15
Графит 10–15
Силициум 11,68
Силициум нитрид 7–8 (поликристален, 1 MHz)[5][6]
Амонијак 26, 22, 20, 17
(−80, −40, 0, +20 °C)
Метанол 30
Етилен гликол 37
Фурфурал 42
Глицерол 41,2, 47, 42,5
(0, 20, 25 °C)
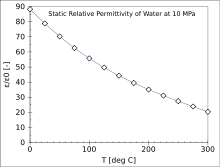
Вода 88, 80,1, 55,3, 34,5
(0, 20, 100, 200 °C)
за видлива светлина: 1,77
Флуороводородна киселина 175, 134, 111, 83,6
−73 °C, −42 °C, −27 °C, 0 °C),
Хидразин 52,0 (20 °C),
Формамид 84,0 (20 °C)
Сулфурна киселина 84–100
(20–25 °C)
Водороден пероксид 128 воден раствор–60
(−30–25 °C)
Цијановодородна киселина 158,0–2,3
(0–21 °C)
Титан диоксид 86–173
Стронциум титанат 310
Бариум стронциум титанат 500
Бариум титанат[7] 1200–10.000
(20–120 °C)
Олово цирконат титанат 500–6000
Конјугирани полимери 1,8–6 up to 100.000[8]
Калциум бакар титанат >250.000[9]

Релативна диелектрична константа на материјалот е неговата (апсолутна) диелектричност изразена како релативен однос на диелектричноста во вакуум

Температурна зависност на релативната статични permittivity на вода

Диелектричноста е материјално својство што влијае на Кулоновата сила помеѓу два точкести полнежи во материјалот. Релативната диелектричност  е факторот за кој електричното поле меѓу полнежите се намалува во однос на полето во вакуум.

Исто така, релативната диелектричност е односот на капацитетот на кондензаторот користејќи го тој материјал како диелектричен, Релативната диелектричност е позната како диелектрична константа поим кој се користи во физиката и инженерството[10] и исто така во хемијата.[11]

Дефиниција

уреди

Релативната диелектричност е обично позната како εr(ω) (понекогаш κ или K) и се дефинира како:

 

каде ε(ω) е комплексна честота зависна од апсолутната диелектричност на материјалот, и ε0 е диелектричност во вакуум[12]

 

Релативната диелектричност на медиум е поврзана со неговиота електрична подложност, χe, како εr(ω) = 1 + χe.

Во анизотропни медиуми (како што се не-кубни кристали) Релативната диелектричност е втор ранг на тензор

Релативната диелектричност на материјал за честота нула е познат како нејзината статична релативна диелектричност.

Терминологија

уреди

Историскиот поим за релативната диелектрична константа е диелектрична константа.[10][11] поради својата недореченост, и бидејќи дел од постарите автори на книги го користеле поимот апсолутна диелектричност ε.[10][13][14] Релативната диелектрична константа може да се дефинира како статичко својство ма честотно зависната променлива. Се користи и за именување на реалниот дел на ε'r на комплексната релативна диелектричност.

Физика

уреди

Во причната теорија на бранови, диелектричноста е сложен квантитет. Имагинарниот дел одговара на фазна промена на поларизација P во однос на E и доведува до намалување на електромагнетни бранови koi  минуваat низ медиумот. По дефиниција, линеарна релативна диелектричност во вакуум е еднаква на 1,[14] која е ε = ε0, иако постојат теоретски нелинеарни квантните ефекти во вакуум кои се не-занемарлива во високо поле.[15]

Следнава табела дава некои типични вредности.

Диелектрични константи на некои растворувачи
Растворувач Диелектрична
Константа 		Температура / К
бензен 2,3 298
диетилетер 4,3 293
тетрахидрофуран (THF) 7,6 298
дихлорометан 9,1 293
течен амонијак 17 273
етанол 24,3 298
метанол 32,7 298
нитрометан 35,9 303
диетил формамид (DMF) 36,7 298
ацетон нитрит 37,5 293
вода 78,7 298
формамид 109 293

Мерење

уреди

Релативната статичнa диелектричност, εr, може да се мери за статични електрични полиња како што се: прво капацитетот на тест кондензаторот, C0, се мери со вакуум меѓу своите плочи. Потоа, користејќи го истиот кондензатор и растојанието помеѓу неговите плочи,се мери  капацитетот C со диелектричност помеѓу плочите. Релативната диелектричност може да биде пресметана како

 

За време-варијанта електромагнетните полиња, ова количество станува честотно-зависно. Една индиректна техника за да се пресмета εr е претворање на радиочестота S-параметар за мерење на резултати. Опис на често користените S-параметар конверзии за определување на честотната зависност од εr на диелектричност може да се најде во библиографските извори.[16] Алтернативно, резонанца врз основа на ефекти може да се внесат на фиксни честоти.[17]

Примена

уреди

Енергија

уреди

Релативната диелектричност е суштински дел од информациите при дизајнирање кондензатори, и во други околности каде материјалот може да се очекува да се воведе капацитет во коло. Ако еден материјал со висока релативна диелектричност е сместен во електричното поле, големината на тоа поле ќе биде мерливо намалена во рамките на обемот на диелектричноста. Овој факт најчесто се користи за да се зголеми капацитетот на одреден кондензаторски дизајн. Слоевите под гравирани диригентни спроводници во печатени кола исто така се однесуваат како диелектрични.

Комуникација

уреди

Диелектричноста се користи во RF преносni линии. Во коаксијален кабел, полиетиленот може да се користи помеѓу централниот спроводник и надвор од штитот. Исто така, може да бидат ставени внатре  во брановоди и да се формираат филтри. Оптичките влакна се примери на диелектрични брановоди. Тие се состојат од диелектрични материјали кои се намерно свешани со нечистотии, па се контролира точната вредност на εr  во рамките на пресек. Ова го контролира показателот на прекршување на материјалот исто така и  оптичкиот начини на пренос. Меѓутоа, во овие случаи, тоа е технички релативната диелектричност која е значајна, како што тие не се управувани во електростатичката граница.

Животна средина

уреди

Релативната диелектричност на воздухот се менува со температурата, влажноста на воздухот, како и барометричкиот притисок.[18] Сензори може да бидат конструирани за откривање на промени во капацитетите предизвикани од промените во релативната диелектричност. Поголемиот дел од оваа промена се должи на ефектите од температурата и влажноста на воздухот, кога барометричниот притисок е прилично стабилен. Користење на капацитетните промени, заедно со измерената температурата, релативната влажност може да се добие со користење на инженерски формули.

Хемија

уреди

Релативната статична диелектричност на растворувач е релативна мерка на својот хемиски поларитет. За пример, водата е многу поларна, и има релативно статична диелектричност од 80.10 на 20 °C, додека n-hexane е не-поларна, и има релативно статична диелектричност од 1.89 на 20 °C.[19] Оваа информација е важна при дизајнирање поделба, примерок за подготовка и хроматографија техники во аналитичка хемија.

Корелација треба, сепак, да се третира со претпазливост. На пример, дихлорометанот има вредност на εr на 9.08 (20 °C) и е прилично слабо растворлив во вода (13 g/L или 9.8 mL/L на 20 °C); во исто време, тетрахидрофуранот има свои εr = 7.52 на 22 °C, но тоа е целосно смешан со вода. Во случај тетрахидрофуранот, кислородниот атом може да дејствува како водороден акцептор; каде што дихлорометанот не може да формира водородна врска со водата.

Ова е дури и повеќе од очигледна кога ќе се направи споредба на εr вредноста на оцетната киселина (6.2528)[20] и  на јодоетанот (7.6177). Големата бројчена вредност на εr не е изненадувачка, во вториот случај, кога атомот на јод  е лесно поларизирачки; сепак, ова не значи дека тоа е поларно, (електронска поларизирачка моќ преовладува над првата оријентација во овој случај).

Губитоци во средината на простирање

уреди

Повторно, слично на  апсолутната диелектричност, релативната диелектричност за загубениот медиум може да се формулира како:

 

во смисла на "диелектричната спроводливост" σ (единици S/m, сименс по метар), кои "суми над сите дисипативни ефекти на материјалот; тоа може да претставува вистинска [електрична] спроводливост предизвикана од миграционо полнење на кариери и тоа исто така може да предизвика енергетска загуба поврзана со дисперзија на ε' [реалната диелектрична вредност]" ( стр. 8). Проширување на аголна честота ω = 2 π c / λ и електричната константа ε0 = 1/(µ0 c2), со што се намалува со:

 

каде што λ е на бранова должина, c е брзината на светлината во вакуум и κ = µ0 c / (2 π) = 59.95849 Ω ≈ 60.0 Ω е новa воведенa константа (единици омови или реципрочната сименс, како што т λ κ = εr останува безединици).

Метали

уреди

Диелектричноста е обично поврзана со диелектрични материјали, сепак металите се опишани како елементи што има ефикасна диелектричност, со вистинска релативна диелектричност еднаква на еден.[21] Во нискочестотен регион, кој се протега од радиочестоти за далеку инфрацрвена и THZ регионот, плазма честотата на електронскиот гас е многу поголема отколку честотата на електромагнетното ширење, па рефракциониот индекс n на металот е скоро чисто имагинарен број. Во нискочестотен режим, ефикасната релативна диелектричност е речиси целосно имагинарна: има многу голема имагинарна вредност, поврзани со спроводливост и релативно незначителна вистинска вредност.[22]

Поврзано

уреди

Наводи

уреди
  1. ↑ Hector, L. G.; Schultz, H. L. (1936). „The Dielectric Constant of Air at Radiofrequencies“. Physics. 7 (4): 133–136. Bibcode:1936Physi...7..133H. doi:10.1063/1.1745374.
  2. ↑ 2,0 2,1 2,2 Young, H. D.; Freedman, R. A.; Lewis, A. L. (2012). University Physics with Modern Physics (13th. изд.). Addison-Wesley. стр. 801. ISBN 978-0-321-69686-1.
  3. ↑ Gray, P. R.; Hurst, P. J.; Lewis, S. H.; Meyer, R. G. (2009). Analysis and Design of Analog Integrated Circuits (5th. изд.). Wiley. стр. 40. ISBN 978-0-470-24599-6.
  4. ↑ Harman, A. K.; Ninomiya, S.; Adachi, S. (1994). „Optical constants of sapphire (α‐Al2O3) single crystals“. Journal of Applied Physics. 76 (12): 8032–8036. Bibcode:1994JAP....76.8032H. doi:10.1063/1.357922.
  5. ↑ „Fine Ceramics“ (PDF). Toshiba Materials.
  6. ↑ „Material Properties Charts“ (PDF). Ceramic Industry. 2013.
  7. ↑ „Permittivity“. schools.matter.org.uk. Архивирано од изворникот на 2016-03-11.
  8. ↑ Pohl, H. A. (1986). „Giant polarization in high polymers“. Journal of Electronic Materials. 15 (4): 201. Bibcode:1986JEMat..15..201P. doi:10.1007/BF02659632.
  9. ↑ Guillemet-Fritsch, S.; Lebey, T.; Boulos, M.; Durand, B. (2006). „Dielectric properties of CaCu3Ti4O12 based multiphased ceramics“ (PDF). Journal of the European Ceramic Society. 26 (7): 1245. doi:10.1016/j.jeurceramsoc.2005.01.055.
  10. ↑ 10,0 10,1 10,2 IEEE Standards Board (1997). „IEEE Standard Definitions of Terms for Radio Wave Propagation“. стр. 6.
  11. ↑ 11,0 11,1 Braslavsky, S.E. (2007). „Glossary of terms used in photochemistry (IUPAC recommendations 2006)“ (PDF). Pure and Applied Chemistry. 79: 293–465. doi:10.1351/pac200779030293.
  12. ↑ Linfeng Chen & Vijay K. Varadan (2004). Microwave electronics: measurement and materials characterization. John Wiley and Sons. стр. 8, eq.(1.15). doi:10.1002/0470020466. ISBN 0-470-84492-2.
  13. ↑ King, Ronold W. P. (1963). Fundamental Electromagnetic Theory. New York: Dover. стр. 139.
  14. ↑ 14,0 14,1 John David Jackson (1998). Classical Electrodynamics (Third. изд.). New York: Wiley. стр. 154. ISBN 0-471-30932-X.
  15. ↑ Mourou, Gerard A. (2006). „Optics in the relativistic regime“. Reviews of Modern Physics. 78: 309. Bibcode:2006RvMP...78..309M. doi:10.1103/RevModPhys.78.309.
  16. ↑ Kuek, CheeYaw. „Measurement of Dielectric Material Properties“ (PDF). R&S.
  17. ↑ Costa, F.; Amabile, C.; Monorchio, A.; Prati, E. (2011). „Waveguide Dielectric Permittivity Measurement Technique Based on Resonant FSS Filters“ (PDF). IEEE Microwave and Wireless Components Letters. 21 (5): 273. doi:10.1109/LMWC.2011.2122303.
  18. ↑ 5×10−6/ºC, 1.4×10−6/%RH and 100×10−6/atm respectively. See A Low Cost Integrated Interface for Capacitive Sensors, Ali Heidary, 2010, Thesis, p. 12.
  19. ↑ Lide, D. R., уред. (2005). CRC Handbook of Chemistry and Physics (LXXXVI. изд.). Boca Raton (FL): CRC Press. ISBN 0-8493-0486-5.
  20. ↑ AE. Frisch, M. J. Frish, F. R. Clemente, G. W. Trucks. Gaussian 09 User's Reference. Gaussian, Inc.: Walligford, CT, 2009.- p. 257.
  21. ↑ Lourtioz, J.-M.; и др. (2005). Photonic Crystals: Towards Nanoscale Photonic Devices. Springer. стр. 121–122. ISBN 3-540-24431-X.
  22. ↑ Lourtioz (2005), equations (4.8)–(4.9), page 122
Преземено од „https://mk.wikipedia.org/w/index.php?title=Релативна_диелектрична_константа&oldid=5245717“