Википедија

Ѕвездена паралакса

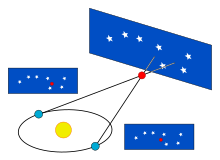
Ѕвездена паралакса — привидното поместување во положбата на една блиска ѕвезда (или друг објект) сопоставена со далечните објекти. Се јавува во различните орбитални положби на Земјата како крајно мало поместување кое е најголемо во интервал од шест месеци, кога Земјата доаѓа на спротивната страна од Сонцето во орбитата, давајќи појдовно растојание од околу две астрономски единици помеѓу набљудувањата. Самата паралакса се смета за половина од најголемата вредност, приближно еквивалентна на набљудателното поместување кое би се јавило поради различните положби на Земјата и Сонцето, што е појдовница од една астрономска единица (ае).

Ѕвездено паралаксно движење од годишна паралакса.
Ѕвездената паралакса е појдовна основа за парсекот — растојанието од Сонцето до извесен астрономски објект кој има паралаксен агол од една лачна секунда. (1 ае и 1 парсек се вон размер; 1 парсек = ~206.265 ае)

Ваквата паралакса тешко се утврдува и затоа нејзинојто постоење било предмет на повеќевековна расправа. За првпат е утврдена во 1806 г. од италијанскиот астроном Џузепе Каландрели, кој забележал паралакса во α Лира (Вега) во неговото дело „Набљудување и осврт на годишната паралакса од Алфа Лира“ (Osservazione e riflessione sulla parallasse annua dall’alfa della Lira).[1] Подоцна, ов 1838 г. германскиот астроном Фридрих Бесел го направил првото успешно мерење на паралакса, за ѕвездата 61 Лебед, користејќи Фраунгоферов хелиометар (сонцемер) во Кенигсбершката опсерваторија.[2][3]

Штом е позната паралаксата на една ѕвезда, нејзината оддалеченост од Земјата може да се пресмета тригонометриски. Меѓутоа, паралаксата се намалува со оддалеченоста на објектот. Дури и во XXI век, астрометријата тешко се справува со растојанија поголеми од 100 парсеци (околу 300 светлосни години), бидејќи добиените вредности се премногу неуточнети за да бидат од корист. Ова става граница на применливоста на паралаксата како мерило за растојанието на објектите кои се релативно блиски во галактички размер. Пооддалечените објекти подобро се мерат со други постапки како со стандардна свеќа и по пат на спектрално црвено поместување.

Ѕвездената паралакса се изразува во многу ситни единици како лачни секунди, па дури и илјадинки од лачни секунди (лачни милидекунди). Далечинскаата единица парсек се дефинира како должината на кракот на прав агол соседен на аголот од една лачна секунда во едно теме, каде другиот краг е долг 1 ае. Бидејќи овие мерења подразбираат многу тенки правоаголни триаголници, пресметувачот е потпомогнат со тригонометриски заокружувања за да се претворат паралаксите (во лачни секунди) во растојание (во парсеци). Приближното растојание просто претставува реципрочна вредност на паралаксата: На пример, Проксима Кентаур (најблиската ѕвезда вон Сончевиот Систем), чија паралакса изнесува 0,7685, е оддалечена 1 / 0,7685 parsecs = 1,301 пс (4,24 сг).[4]

Првични теории и обиди

уреди
 
Долондов хелиометар, 1790 г.

Ѕвезденат паралакса е толку малаа (незабележлива сè до XIX век) што нејзиното привидно отсуство послужило како научен аргумент против хелиоцентризмот во раното нововековие. Според Евклидовата геометрија се гледа дека ефектот би бил незабележлив ако ѕвездата е достатно далеку, но таквите гигантски растојанија се чинеле неверојатни: ова било меѓу главните примедби на Тихо Брахе упатени кон Коперниковиот хелиоцентризам — дека отсуството на ѕвездена паралакса му пркоси на неговиот модел бидејќи тоа би подразбирало постоење на огромна и малку веројатна празнина помеѓу орбитата на Сатурн и осмата сфера (непроменливите ѕвезди).[5]

Англискиот астроном Џејмс Бредли во 1729 г. прв направил напор да измери ѕвездени паралакси. Иако движењето на ѕвездите се покажало како премногу незначајно за неговиот телескоп, Бредли во оваа прилика, наместо тоа, ги открил аберацијата на светлината[6] и нутацијата на Земјината оска, а воедно каталогизирал 3.222 ѕвезди.

XIX и XX век

уреди
 
Беселов хелиометар
 
Поделената леќа на Бамбершкиот хелиометар (крај на XIX век).

Ѕвездената паралакса најчесто се изразува како годишна паралакса, што е положбената разлика на една ѕвезда гледата од Земјата и Сонцето, т.е. аголот кој зафатен во ѕвездата од средниот полупречник на Земјината орбита околу Сонцето. Парсекот (3,26 светлосни години) се дефинира како растојанието при кое годишната паралакса изнесува 1 лачна секунда. Годишната паралакса вообичаено се мери со набљудување на положбата на една ѕвезда во разни времиња од годината додека Земјата се движи по својата орбита. Ова станал првиот доверлив начин за утврдување на оддалеченоста на блиските ѕвезди. Првите успешни мерења на ѕвездената паралакса ги направил Фридрих Бесел во 1838 г. за ѕвездата 61 Лебед со помош на хелиометар.[2][7]

Поради тешката измерливост, кон крајот на XIX век биле познати паралаксите на само 60 ѕвезди, претежно со употреба на нишкест микрометар. На почетокот на XX век овој процес станал многу полесен со употреба на астрографи со фотографски плочи. Во 1960-тите се воведени машини за автоматско мерење на плочите и пософистицирана сметачка технологија[8], со што се овозможило поделотворно составување на ѕвездени каталози. во 1980-тите, фотографските плочи биле заменети со уреди со набојна врска (CCD), сведувајќи ја оптичката неуточнетост на една лачна милисекунда.

Денес ѕвездената паралакса и понатаму претставува стандард при баждарењето на други мерни методи. Точните пресметки на далечини според ѕвездена паралакса се условени од познавањето на далечината помеѓу Земјата и Сонцето, која денес е позната со исклучително висока точност благодарејќи на радарските отсјаи од површините на планетите.[9]

Аглите во овие пресметки се мошне мали и затоа се тешки за мерење. Најблиската ѕвезда до Сонцето (и ѕвездата со најголема паралакса), Проксима Кентаур, има паралакса од 0,7685 ± 0,0002 лачни секунди.[4] Овој агол е приближно оној зафатен од објект со пречник од 2 см на растојание од 5,3 км.

Во Куфнеровата опсерваторија (Виена) во 1896 г. е поставен голем хелиометар, со кој се мерело растојанието до други ѕвезди по пат на тригонометриска паралакса.[10] До 1910 г. со овој инструмент се пресметани 16 паралаксни растојанија на ѕвезди, од вкупно 108 познати за науката во тоа време.[10]

Вселенска астрометрија за паралаксата

уреди
 
Мерката за ѕвездено растојание во Млечниот Пат е продолжена за 10 пати со „Хабл“.[11]

Во 1989 г. е пуштен сателитот „Хипаркос“ со главна цел да ги утврдува паралаксите и сопствените движења на блиските ѕвезди. Благодарение на неговите мерења, денес се познати илјадапати повеќе ѕведени паралакси до точност од лачна милисекунда. Сепак, телескопот е способен да мери ѕвезди не подалечни од 1.600 светлосни години, окофшполу 1 % од пречникот на Млечниот Пат.

Широкоаголната камера на „Хабл“ (WFC3) денес има точност од 20 до 40 лачни микросекунди, овозможувајќи доверливи мерења до 3.066 пс (10.000 сг) за мал број ѕвезди.[12] Ова ѝ дава поголема точност на скалата на вселенски растојанија и ги унапредува сознанијата за растојанијата во вселената, сето засновано на димензиите на Земјината орбита.

Вселенската опсерваторија „Гаја“ на Европската вселенска агенција, пуштена на 19 декември 2013 г., мери паралаксни агли до точност од 10 лачни микросекунди за сите умерено сјајни ѕвези, со што дава карта на блиските ѕвезди (а можеби и планети) до растојание од десетици илјади светлосни години од Земјата.[13] Податоците објавени во 2018 г. имаат средна грешка за паралаксите од 15-тиот величински ред за посјајните ѕвезди од 20–40 лачни микросекунди.[14]

Други појдовници

уреди

Статистичка паралакса

уреди

За да се определат средните растојанија на ѕвездите, постојат два начина на моделирање на нивите движења. Обете се нарекуваат статистичка паралакса — едната е бавнопроменлива паралакса, а другата — класична статистичка паралака.

Движењето на Сонцето низ вселенскиот простор дава подолга појдовница која ја зголемува точноста на паралаксните мерења, што се нареквуа бавнопроменлива паралакса. За ѕвездите од дискот на Млечниот Пат, ова е соодветно на средна појдовница од 4 ае годишно, додека пак за ореолни ѕвезди појдовницата е 40 ае годишно. По неколку десетлетија, појдовницата може да биде неколку величински редови поголема од појдовницата Земја–Сонце која се користи за традиционалната паралакса. Меѓутоа, бавнопроменливата паралакса подразбира повисок степен на несигурност поради дополнителната неизвесност во врска со релативната брзина на другите ѕвезди. Оваа неизвесност се намалува кога методот се применува врз примероци од повеќе ѕвезди наеднаш; уточнетоста е обратнопропорционална на квадратниот корен од големината на примерокот.[15]

Средните паралакси и растојанија на голема група ѕвезди можат да се проценат според нивната радијална брзина и сопствено движење. Ова е познато како класична статистичка паралакса. Движењата на ѕвездите се моделираат за да дадат статистичка слика за брзинскиот расејување според нивното растојание.[15][16]

Други паралакси во астрономијата

уреди

Поимот паралакса во астрономијата може да има и други значења. Така, постојат фотометриска, спектроскопска и динамичка паралакса.

Поврзано

уреди

Наводи

уреди
  1. ↑ Hockey, Thomas, уред. (2007). Biographical Encyclopedia of Astronomers. Springer-Verlag New York. ISBN 978-0-387-30400-7.
  2. ↑ 2,0 2,1 Zeilik & Gregory 1998, стр. 44.
  3. ↑ Hirshfeld, Alan W (1 May 2002). Parallax. ISBN 978-0-8050-7133-7. стр. 259.
  4. ↑ 4,0 4,1 Грешка во Lua: bad argument #1 to 'match' (string expected, got nil)
  5. ↑ Погл. стр. 51 од The reception of Copernicus' heliocentric theory: proceedings of a symposium organized by the Nicolas Copernicus Committee of the International Union of the History and Philosophy of Science, Torun, Poland, 1973, ed. Jerzy Dobrzycki, International Union of the History and Philosophy of Science. Nicolas Copernicus Committee; ISBN 90-277-0311-6, ISBN 978-90-277-0311-8
  6. ↑ Buchheim, Robert (4 October 2007). The Sky is Your Laboratory. ISBN 978-0-387-73995-3. стр. 184.
  7. ↑ Bessel, FW, "Bestimmung der Entfernung des 61sten Sterns des Schwans Архивирано на 24 јуни 2007 г." (1838) Astronomische Nachrichten, vol. 16, pp. 65–96.
  8. ↑ CERN paper on plate measuring machine USNO StarScan
  9. ↑ Zeilik & Gregory 1998, § 22-3.
  10. ↑ 10,0 10,1 Habison, Peter (1998). „Astrometry and early astrophysics at Kuffner Observatory in the late 19th century“. Acta Historica Astronomiae. 3: 93–94. ISSN 0003-2670.
  11. ↑ „Hubble stretches the stellar tape measure ten times further“. ESA/Hubble Images. Посетено на 12 April 2014.
  12. ↑ Harrington, J.D.; Villard, Ray (10 April 2014). „NASA's Hubble Extends Stellar Tape Measure 10 Times Farther into Space“. NASA. Посетено на 17 October 2014. Грешка во Lua: bad argument #1 to 'match' (string expected, got nil)
  13. ↑ Henney, Paul J. „ESA's Gaia Mission to study stars“. Astronomy Today. Архивирано од изворникот на 2008-03-17. Посетено на 8 March 2008.
  14. ↑ Грешка во Lua: bad argument #1 to 'match' (string expected, got nil)
  15. ↑ 15,0 15,1 Popowski, Piotr; Gould, Andrew (29 January 1998). Mathematics of Statistical Parallax and the Local Distance Scale. arXiv:astro-ph/9703140. Bibcode:1997astro.ph..3140P.
  16. ↑ Грешка во Lua: bad argument #1 to 'match' (string expected, got nil)

Литература

уреди
Преземено од „https://mk.wikipedia.org/w/index.php?title=Ѕвездена_паралакса&oldid=5233580“