Тројанец (астрономија)
Тројанец — мало небесно тело (најчесто астероид) кое дели орбита со поголемо тело и останува во стабилна орбита околу 60° пред или зад главното тело близу една од неговите Лагранжови точки L4 и L5. Можат да ги делат орбитите на планети или на големи месечини.
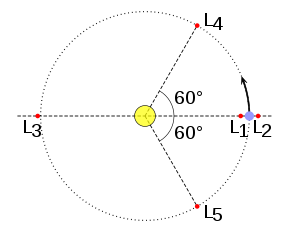
Тројанците се еден вид на коорбитално тело. Во оваа поставеност, една ѕвезда и една планета кружат околу заедничко тежиште, кое е блиску до средиштето на ѕвездата бидејќи таа е обично многу помасивна од кружечката планта. Од своја страна пак, ммогу помала маса од ѕвездата и планетата, сместена во една од Лагранжовите точки на системот ѕвезда-планета, претрпува збирна гравитациска сила која делува преку ова тежиште. Затоа, најмалото тело кружи околу тежиштето со истиот орбитален период како планетата, и составот може да остане стабилен низ времето.[1]
Во Сончевиот Систем, највеќето познати тројанци ја делат орбитата на Јупитер. Поделени се на Грчки табор во L4 (пред Јупитер) и Тројански табор во L5 (зад Јупитер). Се смета дека постојат преку милион Јупитерови тројанци поголеми од еден километар,[2] од кои повеќе од 7.000 денес се каталогизирани. Во другите планетарни орбити до денес се пронајдени само 9 Марсови тројанци, 28 Нептунови тројанци, два Уранови тројанци и еден Земјин тројанец. Познат е и еден привремен Венерин тројанец. Бројчените симулации на орбиталната динамика покажуваат дека Сатурн и Уранверојатно немаат изворни тројанци.[3]
Истата поставеност може да се јави кога главното тело е планета, а споредното е една од месечините, каде многу помалите тројански месечини може да ја имаат неговата орбита. Сите познати тројански месечини се дел од Сатурновиот систем. Телесто и Калипсо се тројанци на Тетида, а Елена и Полидевк на Диона.
Тројански астероиди
уреди| Јупитерови тројанци | Астероиден појас | Хилдски астероиди |
Во 1772 г. италијанско-францускиот математичар и астроном Жозеф-Луј Лагранж дошол до две решенија (колинеарно и рамнострано) на општиот проблем на три тела.[4] Во ограничениот проблем на три тела, со една занемарлива маса (која Лагранж не ја зел предвид), петте можни положби на таа маса денес се наречени Лагранжови точки.
Поимот „тројанец“ првично се однесувал на тројанските астероиди (Јупитеровите тројанци) кои орбитираат блиску до Лагранжовите точки на Јупитер. Уште одамна тие се наречени по ликови од Тројанската војна во старогрчката митологија. По договорен обичај, астероидите кои кружат близу точката L4 на Јупитер се наречени по јунаци од грчката страна на војната, а оние што кружат близу L5 на Јупитер се наречени по јунаците од тројанската страна. Постојат два исклучока, кои ги добиле имињата пред да биде воведен обичајот — 624 Хектор (кој е на грчка страна) и 617 Патрокле (на тројанска).[5]
Астрономите проценуваат дека бројот на Јупитеровит тројанци е приближно еднаков на бројот на астероиди во астероидниот појас.[6]
Подоцна се пронајдени тела кои кружат близу Лагранжовите точки на Нептун, Марс, Земјата,[7] Уран и Венера. Астероидите во Лагранжовите точки на другите планети освеј Јупитер можат да се наречат „Лагранжови астероиди“ или „Лагранжови мали планети“.[8]
- Познати се четири Марсови тројанци: 5261 Еурека, (101429) 1998 VF31, (311999) 2007 NS2 и (121514) 1999 UJ7 — единственото тројанско тело во водечкиот „облак“ во L4,[9][10] Се смета дека тука се присутни и 2001 DH47, 2011 SC191 и 2011 UN63, иако тие сè уште не се прифатени од Центарот за мали планети.
- Познати се 28 Нептунови тројанци,[11] нно поголемите меѓу нив се очекува да бидат десеткратно побројни од Јупитеровите тројанци.[12][13]
- 2010 TK7 е потврден како првиот познат Земјин тројанец во 2011 г. Сместен е во Лагранжовата точка L4, која се наоѓа пред Земјата.[14]
- 2011 QF99 е утврден како првиот Уранов тројанец во 2013 г. Сместен е во Лагранжовата точка L4. Во 2007 г. е пронајден и втор — 2014 YX49.[15]
- 2013 ND15 е привремен Венерин тројанец — првиот од тој вид.
- Големите астероиди Церера и Веста имаат привремени тројанци.[16]
Стабилност
уредиДали системот од ѕвезда, планета и тројанец ќе биде стабилен зависи од големината на растројувањата кои ги претрпува. Ако, на пример, планетата има маса колку Земјата, а околу таа ѕвезда кружи и тело со маса на Јупитер, орбитата на тројанецот ќе биде многу помалку стабилна отколку кога втората планета би била со маса на Плутон.
Како општо правило, системот веројатно ќе биде долговечен ако m1 > 100m2 > 10.000m3 (каде m1, m2 и m3 се масите на ѕвездата, планетата и тројанецот).
Поформално изразено, во тричлен систем со кружни орбити, условот за стабилност е 27(m1m2 + m2m3 + m3m1) < (m1 + m2 + m3)2. Така, бидејќи тројанецот е прашинка, m3→0, налага пониска граница на m1m2 од 25+√6212 ≈ 24,9599. Ако ѕвездата е хипермасивна, m1→+∞, тогаш под дејство на Њутновата гравитација, системот ќе биде стабилен без оглед на масите на планетата и тројанецот. Ако m1m2 = m2m3, тогаш двете мора да надминуваат 13+√168 ≈ 25,9615. Сепак, сето ова претпоставува систем од три тела; ако има повеќе тела (макар и да се далечни и мали) стабилноста на системот бара уште поголеми соодноси.
Поврзано
уредиНаводи
уреди- ↑ Robutel, Philippe; Souchay, Jean (2010), „An introduction to the dynamics of trojan asteroids“, Во Dvorak, Rudolf; Souchay, Jean (уред.), Dynamics of Small Solar System Bodies and Exoplanets, Lecture Notes in Physics, 790, Springer, стр. 197, ISBN 978-3-642-04457-1
- ↑ Yoshida, F.; Nakamura, T. (декември 2005). „Size Distribution of Faint Jovian L4 Trojan Asteroids“. The Astronomical Journal. 130 (6): 2900–2911. doi:10.1086/497571.
- ↑ Sheppard, Scott S.; Trujillo, Chadwick A. (June 2006). „A Thick Cloud of Neptune Trojans and their Colors“ (PDF). Science. 313 (5786): 511–514. Bibcode:2006Sci...313..511S. doi:10.1126/science.1127173. PMID 16778021.
- ↑ Lagrange, Joseph-Louis (1772). „Essai sur le Problème des Trois Corps“ [Essay on the Three-Body Problem] (PDF) (француски). Архивирано од изворникот (PDF) на 22 декември 2017. Наводот journal бара
|journal=(help) - ↑ Wright, Alison (1 август 2011). „Planetary science: The Trojan is out there“. Nature Physics. 7 (8): 592. Bibcode:2011NatPh...7..592W. doi:10.1038/nphys2061.
- ↑ Yoshida, Fumi; Nakamura, Tsuko (2005). „Size distribution of faint L4 Trojan asteroids“. The Astronomical Journal. 130 (6): 2900–11. Bibcode:2005AJ....130.2900Y. doi:10.1086/497571.
- ↑ Connors, Martin; Wiegert, Paul; Veillet, Christian (27 јули 2011). „Earth's Trojan asteroid“. Nature. 475 (7357): 481–483. Bibcode:2011Natur.475..481C. doi:10.1038/nature10233. PMID 21796207.
- ↑ Whiteley, Robert J.; Tholen, David J. (ноември 1998). „A CCD Search for Lagrangian Asteroids of the Earth–Sun System“. Icarus. 136 (1): 154–167. Bibcode:1998Icar..136..154W. doi:10.1006/icar.1998.5995.
- ↑ „List of Martian Trojans“. Minor Planet Center. Посетено на 3 јули 2015.
- ↑ de la Fuente Marcos, C.; de la Fuente Marcos, R. (15 мај 2013). „Three new stable L5 Mars Trojans“. Letters. Monthly Notices of the Royal Astronomical Society. 432 (1): 31–35. arXiv:1303.0124. Bibcode:2013MNRAS.432L..31D. doi:10.1093/mnrasl/slt028.
- ↑ „List of Neptune Trojans“. Minor Planet Center. 28 октомври 2018. Посетено на 28 декември 2018.
- ↑ Chiang, Eugene I.; Lithwick, Yoram (20 јули 2005). „Neptune Trojans as a Testbed for Planet Formation“. The Astrophysical Journal. 628 (1): 520–532. arXiv:astro-ph/0502276. Bibcode:2005ApJ...628..520C. doi:10.1086/430825.
- ↑ Powell, David (30 јануари 2007). „Neptune May Have Thousands of Escorts“. Space.com.
- ↑ Choi, Charles Q. (27 јули 2011). „First Asteroid Companion of Earth Discovered at Last“. Space.com. Посетено на 27 јули 2011.
- ↑ de la Fuente Marcos, Carlos; de la Fuente Marcos, Raúl (21 мај 2017). „Asteroid 2014 YX49: a large transient Trojan of Uranus“. Monthly Notices of the Royal Astronomical Society. 467 (2): 1561–1568. arXiv:1701.05541. Bibcode:2017MNRAS.467.1561D. doi:10.1093/mnras/stx197.
- ↑ Christou, Apostolos A.; Wiegert, Paul (јануари 2012). „A population of main belt asteroids co-orbiting with Ceres and Vesta“. Icarus. 217 (1): 27–42. arXiv:1110.4810. Bibcode:2012Icar..217...27C. doi:10.1016/j.icarus.2011.10.016.
Надворешни врски
уреди- Тројанци, списание „Квант“ (руски)