Ѕвездена структура

Моделите на ѕвездената структура подробно ја опишуваат внатрешната структура на ѕвездата и даваат предвидувања за сјајноста, бојата и идната еволуција на ѕвездата. Различни класи и возрасти на ѕвезди имаат различни внатрешни структури, како одраз на нивната елементарна структура и механизми за пренос на енергија.

Пренос на топлина

За пренос на енергија погледнете во зрачен пренос.

Различните преносни механизми на ѕвезди со голема, средна и мала маса.

Различните слоеви на ѕвездите го пренесуваат загревањето и нанадвор на различни начини, првенствено конвекција и зрачен пренос, но топлинската спроводливост е важна кај белите џуџиња.

Конвекцијата е главен начин на пренос на енергија кога температурниот градиент е доволно нагол, така што одреден волумен гас во ѕвездата ќе продолжи да расте ако малку се подигне преку адијабатска постапка. Во овој случај, волуменот што расте е пловен и продолжува да расте ако е потопол од околниот гас; ако волуменот што расте е поладен од околниот гас, тој ќе се врати на првобитната висина.^[1] Во региони со низок температурен градиент и доволно ниска непроѕирност за да биде овозможен пренос на енергија преку зрачење, зрачењето е главен начин на пренос на енергија.

Внатрешната структура на ѕвездата од главната низа зависи од масата на ѕвездата.

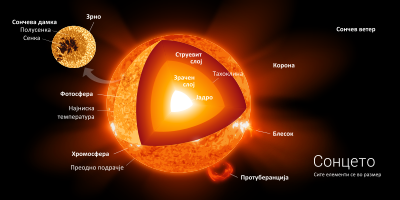
Кај ѕвездите со маса од 0,3-1,5 сончеви маси (M_☉, вклучувајќи го и Сонцето, соединувањето на водород со хелиум се случува првенствено преку протонско-протонски ланци, кои не воспоставува нагол температурен градиент. Така, зрачењето надвладејува во внатрешниот дел на ѕвездите со сончева маса. Надворешниот дел од ѕвездите со сончева маса е доволно ладен што водородот е неутрален и на тој начин непроѕирен за ултравиолетовите фотони, па така надвладејува конвекцијата. Според тоа, ѕвездите со сончева маса имаат зрачни јадра со конвективни обвивки во надворешниот дел на ѕвездата.

Кај масивните ѕвезди (поголеми од околу 1,5 M☉), температурата на јадрото е над околу 1,8 × 10⁷ К, така што соединувањето на водород со хелиум се случува првенствено преку циклусот јаглерод-азот-кислород. Во овој циклус, стапката на производство на енергија е рангирана како температура до 15-та моќност, додека стапката е рангирана како температура до 4-та моќност во протонско-протонските ланци.^[2] Поради силната температурна чувствителност на циклусот јаглерод-азот-кислород, температурниот градиент во внатрешниот дел на ѕвездата е доволно стрмен за да го направи јадрото струевито. Во надворешниот дел на ѕвездата, температурниот градиент е поплиток, но температурата е доволно висока што водородот е речиси целосно јонизиран, така што ѕвездата останува проѕирна за ултравиолетовото зрачење. Така, масивните ѕвезди имаат зрачна обвивка.

Ѕвездите од главната низа со најмала маса немаат зона на зрачење; доминантен механизам за преност на енергија низ ѕвездата е конвекцијата.^[3]

Равенки на ѕвездената структура

Температурен профил во Сонцето.

Маса внатре во даден полупречник во Сонцето.

Профил на густина во Сонцето.

Профил на притисок во Сонцето.

Наједноставниот најчесто користен модел на ѕвездена структура е сферично симетричниот квазистатички модел, кој претпоставува дека ѕвездата е во стабилна состојба и дека е сферично симетрична. Содржи четири основни диференцијални равенки од прв ред: две претставуваат како материјата и притисокот варираат со полупречникот; два претставуваат како температурата и сјајноста варираат со полупречникот.^[4]

При образувањето на равенките на ѕвездената структура (искористувајќи ја претпоставената сферична симетрија), земена е во предвид густината на материјата $\rho (r)$ , температура $T(r)$ , вкупен притисок (материја плус зрачење) $P(r)$ , сјајност $l(r)$ , и стапка на производство на енергија по единица маса $\epsilon (r)$ во сферична обвивка со дебелина ${\mbox{d}}r$ на далечина $r$ од средиштето на ѕвездата. Се претпоставува дека ѕвездата е во месна термодинамичка рамнотежа (МТР), така што температурата е идентична за материјата и фотоните. Иако МТР не е одржувана строго бидејќи температурата што дадената обвивка ја „гледа“ под себе е секогаш пожешка од температурата горе, оваа приближување е нормално одлична затоа што фотонот значи слободна патека, $\lambda$ , е многу помала од должината по која температурата значително варира, т.е $\lambda \ll T/|\nabla T|$ .

Прво е изјава за „хидростатичка рамнотежа“: надворешната сила поради градиентот на притисокот во ѕвездата е точно урамнотежена со силата навнатре поради гравитацијата. Ова понекогаш е нарекувано ѕвездена рамнотежа.

{{\mbox{d}}P \over {\mbox{d}}r}=-{Gm\rho  \over r^{2}}

,

каде $m(r)$ е собраната маса во внатрешноста на обвивката во $r$ а G е гравитационата константа. Насобраната маса се зголемува со полупречникот според „равенката за продолжение на масата“:

{{\mbox{d}}m \over {\mbox{d}}r}=4\pi r^{2}\rho .

Вклучување на равенката за продолжение на масата од средиштето на ѕвездата ( $r=0$ ) до полупречникот на ѕвездата ( $r=R$ ) ја дава вкупната маса на ѕвездата.

Ако е земен во предвид енергијата што ја напушта сферичната обвивка, добиена е „енергетската равенка“:

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

,

каде $\epsilon _{\nu }$ е сјајноста произведена во облик на неутрина (кои обично бегаат од ѕвездата без да заемодејствуваат со обичната материја) по единица маса. Надвор од јадрото на ѕвездата, каде што се случуваат јадрени реакции, не се создава енергија, па затоа сјајноста е постојана.

Равенката за пренос на енергија има различни облици во зависност од начинот на пренос на енергија. За пренос на спроводлива енергија (соодветно за бело џуџе), равенката на енергијата е

{{\mbox{d}}T \over {\mbox{d}}r}=-{1 \over k}{l \over 4\pi r^{2}},

каде k е топлинска спроводливост.

Во случај на пренос на зрачна енергија, соодветен за внатрешниот дел на ѕвезда од главната низа на сончевата маса и надворешната обвивка на масивна ѕвезда од главната низа,

{{\mbox{d}}T \over {\mbox{d}}r}=-{3\kappa \rho l \over 64\pi r^{2}\sigma T^{3}},

каде $\kappa$ е непроѕирноста на материјата, $\sigma$ е Штефан-Болцмановата константа, а Болцмановата константа е поставена на еден.

Случајот на пренос на конвективна енергија нема позната ригорозна математичка формулација и вклучува турбуленции во гасот. Преносот на конвективната енергија обично е моделиран користејќи теорија на должина на мешање. Ова го третира гасот во ѕвездата како што содржи дискретни елементи кои грубо ја задржуваат температурата, густината и притисокот на нивната околина, но се движат низ ѕвездата до карактеристична должина, наречена „должина на мешање“.^[5] За монатомски идеален гас, кога конвекцијата е адијабатична, што значи дека конвективните гасни меури не разменуваат топлина со нивната околина, теоријата за должина на мешање дава

{{\mbox{d}}T \over {\mbox{d}}r}=\left(1-{1 \over \gamma }\right){T \over P}{{\mbox{d}}P \over {\mbox{d}}r},

каде $\gamma =c_{p}/c_{v}$ е адијабатскиот индекс, односот на засебните жаришта во гасот. (За целосно јонизиран идеален гас, $\gamma =5/3$ .) Кога конвекцијата не е адијабатска, вистинскиот температурен градиент не е даден со оваа равенка. На пример, на Сонцето конвекцијата во основата на зоната на конвекција, во близина на јадрото, е адијабатска, но таа во близина на површината не е. Теоријата за должина на мешање содржи два слободни параметри кои мора да бидат поставени за да биде направен моделот да одговара на набљудувањата, така што тоа е феноменолошка теорија наместо ригорозна математичка формулација.^[6]

Потребни се и состојбените равенки, кои ги поврзуваат притисокот, непроѕирноста и стапката на создавање енергија со други месни променливи соодветни за материјалот, како што се температурата, густината, хемискиот состав итн. Релевантните равенки на состојбата за притисок можеби ќе треба да го вклучат законот за совршен гас, притисок на зрачење, притисок поради изродени електрони итн. Непроѕирноста не може точно да биде изразен со една формула. Пресметуван е за различни композиции при засебни густини и температури и се прикажува во табеларен облик.^[7] „Кодовите“ на ѕвездената структура (што значи сметачки програми кои ги пресметуваат променливите на моделот) или се меѓуполираат во мрежа за густина-температура за да ја добијат потребната непроѕирност или користат функција за прилагодување врз основа на табеларните вредности. Слична ситуација се јавува и за точни пресметки на равенката на притисокот на состојбата. Конечно, стапката на создавање на јадрена енергија е пресметувана од опити по јадрена физика, користејќи „реакциони мрежи“ за да бидат пресметани стапките на реакција за секој поединечен чекор на реакција и рамнотежа изобилство за секој изотоп во гасот.^[6]^[8]

Во комбинација со множество гранични услови, решението на овие равенки целосно го опишува однесувањето на ѕвездата. Типичните гранични услови соодветно ги поставуваат вредностите на набљудуваните параметри на површината ( $r=R$ ) и средиште ( $r=0$ ) на ѕвездата: $P(R)=0$ , што значи дека притисокот на површината на ѕвездата е нула; $m(0)=0$ , нема маса во средиштето на ѕвездата, како што се бара ако масената густина остане конечна; $m(R)=M$ , вкупната маса на ѕвездата е масата на ѕвездата; и $T(R)=T_{eff}$ , температурата на површината е делотворна температура на ѕвездата.

Иако во денешно време моделите на ѕвездената еволуција ги опишуваат главните особини на дијаграмите со обоена јачина, треба да бидат направени важни подобрувања со цел да бидат отстранети неизвесностите кои се поврзани со ограниченото познавање на преносните феномени. Најтешкиот предизвик останува бројчаниот третман на турбуленциите.^{[се бара извор]} Некои истражувачки работни состави развиваат поедноставено моделирање на турбуленции во тридимензионални пресметки.

Брза еволуција

Горенаведениот поедноставен модел не е соодветен без модификација во ситуации кога промените на составот се доволно брзи. Равенката на хидростатската рамнотежа можеби ќе треба да се измени со додавање поим за полупречничко забрзување ако полупречникот на ѕвездата се менува многу брзо, на пример ако ѕвездата полупречнички пулсира.^[9] Исто така, ако јадреното согорување не е стабилно, или јадрото на ѕвездата брзо се распаѓа, мора да биде додаден поим за ентропија на енергетската равенка.^[10]

Поврзано

Наводи

↑ Hansen, Kawaler & Trimble (2004, §5.1.1)
↑ Hansen, Kawaler & Trimble (2004, Tbl. 1.1)
↑ Hansen, Kawaler & Trimble (2004, §2.2.1)
↑ This discussion follows those of, e. g., Zeilik & Gregory (1998, §16-1–16-2) and Hansen, Kawaler & Trimble (2004, §7.1)
↑ Hansen, Kawaler & Trimble (2004, §5.1)
↑ ^6,0 ^6,1 Ostlie, Dale A. and Carrol, Bradley W., An introduction to Modern Stellar Astrophysics, Addison-Wesley (2007)
↑ Iglesias, C. A.; Rogers, F. J. (June 1996), „Updated Opal Opacities“, Astrophysical Journal, 464: 943–+, Bibcode:1996ApJ...464..943I, doi:10.1086/177381.
↑ Rauscher, T.; Heger, A.; Hoffman, R. D.; Woosley, S. E. (септември 2002), „Nucleosynthesis in Massive Stars with Improved Nuclear and Stellar Physics“, The Astrophysical Journal, 576 (1): 323–348, arXiv:astro-ph/0112478, Bibcode:2002ApJ...576..323R, doi:10.1086/341728.
↑ Moya, A.; Garrido, R. (август 2008), „Granada oscillation code (GraCo)“, Astrophysics and Space Science, 316 (1–4): 129–133, arXiv:0711.2590, Bibcode:2008Ap&SS.316..129M, doi:10.1007/s10509-007-9694-2.
↑ Mueller, E. (јули 1986), „Nuclear-reaction networks and stellar evolution codes – The coupling of composition changes and energy release in explosive nuclear burning“, Astronomy and Astrophysics, 162 (1–2): 103–108, Bibcode:1986A&A...162..103M.

Извори

Kippenhahn, R.; Weigert, A. (1990), Stellar Structure and Evolution, Springer-Verlag
Hansen, Carl J.; Kawaler, Steven D.; Trimble, Virginia (2004), Stellar Interiors (2nd. изд.), Springer, ISBN 0-387-20089-4
Kennedy, Dallas C.; Bludman, Sidney A. (1997), „Variational Principles for Stellar Structure“, Astrophysical Journal, 484 (1): 329–340, arXiv:astro-ph/9610099, Bibcode:1997ApJ...484..329K, doi:10.1086/304333
Weiss, Achim; Hillebrandt, Wolfgang; Thomas, Hans-Christoph; Ritter, H. (2004), Cox and Giuli's Principles of Stellar Structure, Cambridge Scientific Publishers, Bibcode:2004cgps.book.....W
Zeilik, Michael A.; Gregory, Stephan A. (1998), Introductory Astronomy & Astrophysics (4th. изд.), Saunders College Publishing, ISBN 0-03-006228-4

Надворешни врски

кодот за непроѕирност пристапен во ноември 2009 година
Жолта CESAM код, ѕвездена еволуција и структура, изворен код на Фортран
EZ to Evolve ZAMS Stars програмска опрема FORTRAN 90 изведен од Елгстоновиот ѕвезден еволуциски код (Eggleton's Stellar Evolution Code), семрежен интерфејс може да се најде овде [1].
Женевски мрежи на модели на ѕвездена еволуција (некои од нив вклучувајќи мешање предизвикано од вртење)
Базата на податоци за еволуција на ѕвездите на BaSTI
Ѕвездени атмосфери: Придонес кон набљудувачко проучување на високата температура во обратните слоеви на ѕвездите, (1925) од Сесилија Пејн-Гапошкин, Кембриџ: The Observatory.

[1] Hansen, Kawaler & Trimble (2004, §5.1.1)

[2] Hansen, Kawaler & Trimble (2004, Tbl. 1.1)

[3] Hansen, Kawaler & Trimble (2004, §2.2.1)

[4] This discussion follows those of, e. g., Zeilik & Gregory (1998, §16-1–16-2) and Hansen, Kawaler & Trimble (2004, §7.1)

[5] Hansen, Kawaler & Trimble (2004, §5.1)

[Ostlie-6] 6,0 ^6,1 Ostlie, Dale A. and Carrol, Bradley W., An introduction to Modern Stellar Astrophysics, Addison-Wesley (2007)

[Rogers1996-7] Iglesias, C. A.; Rogers, F. J. (June 1996), „Updated Opal Opacities“, Astrophysical Journal, 464: 943–+, Bibcode:1996ApJ...464..943I, doi:10.1086/177381.

[Heger2002-8] Rauscher, T.; Heger, A.; Hoffman, R. D.; Woosley, S. E. (септември 2002), „Nucleosynthesis in Massive Stars with Improved Nuclear and Stellar Physics“, The Astrophysical Journal, 576 (1): 323–348, arXiv:astro-ph/0112478, Bibcode:2002ApJ...576..323R, doi:10.1086/341728.

[9] Moya, A.; Garrido, R. (август 2008), „Granada oscillation code (GraCo)“, Astrophysics and Space Science, 316 (1–4): 129–133, arXiv:0711.2590, Bibcode:2008Ap&SS.316..129M, doi:10.1007/s10509-007-9694-2.

[10] Mueller, E. (јули 1986), „Nuclear-reaction networks and stellar evolution codes – The coupling of composition changes and energy release in explosive nuclear burning“, Astronomy and Astrophysics, 162 (1–2): 103–108, Bibcode:1986A&A...162..103M.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]