Впишана кружница

Впишана кружница — во рамнинската геометрија, впишана кружница е кружница што ги има сите страни на даден многуаголник за тангенти. Кругот ограничен со оваа кружница се нарекува впишан круг.

Кружница впишана во триаголник

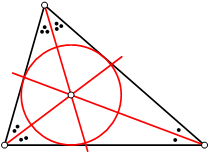
Постоење на впишана кружница

Кружница може да впишеме само во некои многуаголници. Таквите многуаголници се нарекуваат тангентни многуаголници.

Ако двата краци на даден агол се тангенти на круг, тогаш центарот на кругот лежи на симетралата на аголот. Ова ни овозможува да конструираме впишана кружница, како и критериум за тоа кога воопшто постои впишана кружница. Нека е даден многуаголник:

• Прво, ги конструираме симетралите на сите внатрешни агли.
• Ако симетралите на сите агли се сечат во иста точка, тогаш постои впишана кружница и оваа точка е центар на впишаната кружница.
• Полупречникот на впишаната кружница е растојанието помеѓу центарот и која било страна (мерено нормално на таа страна).

Во најновите учебници по математика, полупречникот на впишана кружница секогаш се означува со r, а полупречникот на опишана кружница со R (во постарите учебници, полупречникот на впишана кружница бил ρ, а полупречникот на опишана кружница бил r ).

Некои многуаголници за кои сигурно можеме да впишеме кружница:

• триаголник
• ромб
• делтоид
• правилен многуаголник

Впишана кружница во триаголник

Впишана кружница во триаголник и три припишани кружници на триаголник. Центрите на припишаните кружници се добиваат со симетралите на надворешните агли.

Триаголникот има особеност дека симетралите на внатрешните агли секогаш се сечат во иста точка, така што секогаш можеме да впишеме кружница во триаголник. За полупречникот на впишаната кружница важи следната поврзаност со плоштината (p) на триаголникот:

$r={\frac {p}{s}}\!\,.$

Во овој случај, s е половина од обемот на триаголникот (исто како кај Хероновата формула ): $s={\frac {a+b+c}{2}}$

Впишана кружница во квадрат

Кружница може да се впише само кај некои четириаголници - нив ги нарекуваме тангентни четириаголници.

Тангентните четириаголници се одликуваат со тоа што збировите на спротивните страни им се еднакви:

$a+c=b+d\!\,.$

Полупречникот на впишаната кружница има слична врска со плоштината (p) како и за триаголникот:

$r={\frac {p}{s}}\!\,.$

При што, s е половина периметар на четириаголникот: $s={\frac {a+b+c+d}{2}}$

Поврзано

• Опишана кружница
• Апотема

Надворешни врски

• Derivation of formula for radius of incircle of a triangle
• „Incircle“ од Ерик В. Вајсштајн — MathWorld (англиски)

Интерактивни

• Triangle incenter   Triangle incircle  Incircle of a regular polygon   With interactive animations
• Constructing a triangle's incenter / incircle with compass and straightedge An interactive animated demonstration
• Equal Incircles Theorem at cut-the-knot
• Five Incircles Theorem at cut-the-knot
• Pairs of Incircles in a Quadrilateral at cut-the-knot
• An interactive Java applet for the incenter