Права на Њутн-Гаус

Во геометријата, Њутн-Гаусовата права (или Гаус-Њутновата права) е правата која ги спојува средишните точки на трите дијагонали на комплетен четириаголник.

Средишните точки на двете дијагонали на конвексен четириаголник со најмногу две паралелни страни се различни и на тој начин одредуваат права, наречена Њутнова права. Ако страните на таков четириаголник се продолжат за да формираат комплетен четириаголник, дијагоналите на четириаголникот остануваат дијагонали на комплетниот четириаголник, а Њутновата права на четириаголникот е Њутн-Гаусовата права на комплетниот четириаголник.

Комплетни четириаголници

Секои четири прави во општа положба (меѓу кои нема две паралелни и нема три кои се сечат во иста точка) формираат комплетен четириаголник. Оваа конфигурација се состои од вкупно шест точки, пресечните точки на четирите линии, со три точки на секоја права и точно по две прави низ секоја точка. ^[1] Овие шест точки може да се поделат во парови така што отсечките на правите определени со кој било пар не се сечат со ниту една од дадените четири прави освен во крајните точки. Овие три отсечки се нарекуваат дијагонали на комплетниот четириаголник.

Постоење на правата на Њутн-Гаус

Етикети кои се користат за доказ за целосен четириаголник

Добро е позната теоремата дека трите средишни точки на дијагоналите на комплетен четириаголник се колинеарни.^[2] Постојат неколку докази за резултатот во кои се користат плоштини^[2] или надворешни производи ^[3] или, како следниов доказ, на теоремата на Менелај, која се должи на Хилер и е објавена во 1920 година.^[4]

Нека целосниот четириаголник $ABCA'B'C'$ е означен како на дијаграмот со дијагонали ${\overline {AA'}},{\overline {BB'}},{\overline {CC'}},$ и нивните соодветни средишни точки $L, M, N$ . Нека средните точки на ${BC},CA',{A'B},$ се $P, Q, R$ соодветно. Користејќи слични триаголници, се гледа дека $QR$ ja сече $AA'$ во $L$ , $RP$ ја сече $BB'$ во $M$ и $PQ$ ја сече $CC'$ во $N$ . Повторно, од слични триаголници се добиваат следниве пропорции:

{\frac {\overline {RL}}{\overline {LQ}}}={\frac {\overline {BA}}{\overline {AC}}},\quad {\frac {\overline {QN}}{\overline {NP}}}={\frac {\overline {A'C'}}{\overline {C'B}}},\quad {\frac {\overline {PM}}{\overline {MR}}}={\frac {\overline {CB'}}{\overline {B'A'}}}.

Меѓутоа, правата $AB'C'$ ги сече страните на $△ A'BC$ , така што според теоремата на Менелај, производот на членовите на десната страна е −1. Така, производот на членовите од левата страна е исто така −1 и повторно според теоремата на Менелај, точките $L, M, N$ се колинеарни и се на страните на триаголникот $△ PQR$ .

Примени кај тетивни четириаголници

Следниве резултати се само некои во кои се користи Њутн-Гаусовата права за комплетни четириаголници и кои се поврзани со тетивните четириаголници, врз основа на работата на Барбу и Патраску.^[5]

Еднакви агли

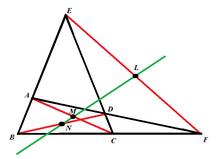
Слика 1: Еднаквост на агли.

За даден тетивен четириаголник $ABCD$ , нека точката $F$ е пресечната точка на двете дијагонали $AC$ и $BD$ . Продолжете ги дијагоналите $AB$ и $CD$ до пресечната точка $E$ . Нека средишната точка на отсечката $EF$ е $N$ , а средната точка на отсечката $BC$ е $M$ (слика 1).

Теорема

Ако средишната точка на отсечката $BF$ е $P$ , Њутн-Гасовата права на комплетниот четириаголник $ABCDEF$ и правата $PM$ одредуваат агол $∠ PMN$ еднаков на $∠ EFD$ .

Доказ

Прво покажете дека $△ NPM$ и $△ EDF$ се слични.

Бидејќи $BE ∥ PN$ и $FC ∥ PM$ , знаеме $∠ NPM = ∠ EAC$ . Исто така, ${\tfrac {\overline {BE}}{\overline {PN}}}={\tfrac {\overline {FC}}{\overline {PM}}}=2.$

Во тетивниот четириаголник $ABCD$ , важат овие еднаквости:

{\begin{aligned}\angle EDF&=\angle ADF+\angle EDA,\\&=\angle ACB+\angle ABC,\\&=\angle EAC.\end{aligned}}

Затоа, $∠ NPM = ∠ EDF$ .

Нека $R 1, R 2$ се радиусите на опишаните кружници околу $△ EDB, △ FCD$ соодветно. Со примена на синусната теорема на триаголниците, се добива:

{\frac {\overline {BE}}{\overline {FC}}}={\frac {2R_{1}\sin \angle EDB}{2R_{2}\sin \angle FDC}}={\frac {R_{1}}{R_{2}}}={\frac {2R_{1}\sin \angle EBD}{2R_{2}\sin \angle FCD}}={\frac {\overline {DE}}{\overline {DF}}}.

Бидејќи $BE = 2 \cdot PN$ и $FC = 2 \cdot PM$ , добиваме дека ${\tfrac {\overline {PN}}{\overline {PM}}}={\tfrac {\overline {DE}}{\overline {DF}}}.$ Следува сличноста на триаголниците $△ PMN, △ DFE$ од каде $∠ NMP = ∠ EFD$ .

Забелешка

Ако $Q$ е средишна точка на отсечката $FC$ , со истото резонирање следи дека $∠ NMQ = ∠ EFA$ .

Слика 2: Изогонални линии.

Изогонални линии

Теорема

Правата низ $E$ паралелна со Њутн-Гаусовата права на комплетниот четириаголник $ABCDEF$ и правата $EF$ се изогонални линии на $∠ BEC$ , т.е. секоја права е слика на другата во однос на симетралата на аголот.^[5] (Слика 2)

Доказ

Триаголниците $△ EDF, △ NPM$ се слични според горенаведениот аргумент, па затоа $∠ DEF = ∠ PNM$ . Нека $E'$ е пресечната точка на $BC$ и правата паралелна на Њутн-Гасовата права $NM$ кој минува низ $E$ .

Бидејќи $PN ∥ BE$ и $NM ∥ EE',$ имаме дека $∠ BEF = ∠ PNF$ и $∠ FNM = ∠ E'EF$ .

Затоа,

{\begin{aligned}\angle CEE'&=\angle DEF-\angle E'EF,\\&=\angle PNM-\angle FNM,\\&=\angle PNF=\angle BEF.\end{aligned}}

Два тетивни четириаголника кои имаат заедничка Њутн-Гаусова права

Слика 3: Четириаголниците

MPGN, MQHN

се тетивни.

Лема

Нека $G$ и $H$ се ортогоналните проекции на точката $F$ врз правите $AB$ и $CD$ соодветно.

Четиристраниците $MPGN$ и $MQHN$ се тетивни четириаголници. ^[5]

Доказ

$∠ EFD = ∠ PMN$ , како што претходно беше покажано. Tочките $P$ и $N$ сe соодветните центри на опишаните кружници на правоаголните триаголници $△ BFG, △ EFG$ . Затоа, $∠ PGF = ∠ PFG$ и $∠ FGN = ∠ GFN$ .

Затоа,

{\begin{aligned}\angle PGN+\angle PMN&=(\angle PGF+\angle FGN)+\angle PMN\\[4pt]&=\angle PFG+\angle GFN+\angle EFD\\[4pt]&=180^{\circ }\end{aligned}}.

Според тоа, $MPGN$ е тетивен четириаголник, и според истото резонирање, $MQHN$ исто така лежи на кружница.

Слика 4: Покажува дека комплетните четириаголници

EDGHIJ, ABCDEF

имаат иста Њутн-Гаусова права.

Теорема

Продолжете ги правите $GF, HF$ до нивните пресеци со $EC, EB$ - во точките $I, J$ соодветно (слика 4).

Комплетните четириаголници $EFGHIJ$ и $ABCDEF$ имаат иста Њутн-Гаусова права.^[5]

Доказ

Двата комплетни четириаголници имаат заедничка дијагонала, $EF$ . $N$ лежи на Њутн-Гаусовата права на двата четириаголника. $N$ е подеднакво оддалечена од $G$ и $H$ , бидејќи е центарот на опишаната кружница околу тетивниот четириаголник $EGFH$ .

Ако триаголниците $△ GMP, △ HMQ$ се складни, па ќе следи дека $M$ лежи на симетралата на правата $HG$ . Според тоа, правата $MN$ ја содржи средишната точка на $GH$ и е Њутн-Гаусова права на $EFGHIJ$ .

За да покажете дека триаголниците $△ GMP, △ HMQ$ се конгруентни, прво забележете дека $PMQF$ е паралелограм, бидејќи точките $M, P$ се средни точки на $BF, BC$ соодветно.

Затоа,

{\begin{aligned}&{\overline {MP}}={\overline {QF}}={\overline {HQ}},\\&{\overline {GP}}={\overline {PF}}={\overline {MQ}},\\&\angle MPF=\angle FQM.\end{aligned}}

Забележете и дека

\angle FPG=2\angle PBG=2\angle DBA=2\angle DCA=2\angle HCF=\angle HQF.

Оттука,

{\begin{aligned}\angle MPG&=\angle MPF+\angle FPG,\\&=\angle FQM+\angle HQF,\\&=\angle HQF+\angle FQM,\\&=\angle HQM.\end{aligned}}

Затоа, $△ GMP$ и $△ HMQ$ се складни според признакот САС.

Забелешка

Поради тоа што $△ GMP, △ HMQ$ се складни триаголници, нивните опишани кружници $MPGN, MQHN$ се исто така складни.

Историја

Доказот за Њутн-Гаусовата права бил развиен од двајцата математичари по кои е именуван: сер Исак Њутн и Карл Фридрих Гаус. Почетната рамка за оваа теорема е од работата на Њутн, во неговата претходна теорема за Њутновата права, во која Њутн покажал дека центарот на кониката впишана во четириаголник лежи на Њутн-Гаусовата права.^[6]

Теоремата на Гаус и Боденмилер вели дека трите кружници чии дијагонали се дијагонали на комплетен четириаголник се коаксални.^[7]

Белешки

↑ Alperin, Roger C. (6 January 2012). „Gauss–Newton Lines and Eleven Point Conics“. Research Gate.
↑ ^2,0 ^2,1 Johnson 2007
↑ Pedoe, Dan (1988) [1970], Geometry A Comprehensive Course, Dover, стр. 46–47, ISBN 0-486-65812-0
↑ Johnson 2007
↑ ^5,0 ^5,1 ^5,2 ^5,3 Patrascu, Ion. „Some Properties of the Newton–Gauss Line“ (PDF). Forum Geometricorum. Архивирано од изворникот (PDF) на 2023-03-29. Посетено на 29 април 2019.
↑ Wells, David (1991), The Penguin Dictionary of Curious and Interesting Geometry, Penguin Books, стр. 36, ISBN 978-0-14-011813-1
↑ Johnson 2007

[:1-1] Alperin, Roger C. (6 January 2012). „Gauss–Newton Lines and Eleven Point Conics“. Research Gate.

[Johson62-2] 2,0 ^2,1 Johnson 2007

[3] Pedoe, Dan (1988) [1970], Geometry A Comprehensive Course, Dover, стр. 46–47, ISBN 0-486-65812-0

[4] Johnson 2007

[:2-5] 5,0 ^5,1 ^5,2 ^5,3 Patrascu, Ion. „Some Properties of the Newton–Gauss Line“ (PDF). Forum Geometricorum. Архивирано од изворникот (PDF) на 2023-03-29. Посетено на 29 април 2019.

[6] Wells, David (1991), The Penguin Dictionary of Curious and Interesting Geometry, Penguin Books, стр. 36, ISBN 978-0-14-011813-1

[7] Johnson 2007

[1]

[2]

[3]

[4]

[5]

[6]

[7]