Единична кружница

Единична кружница

Единична кружница (со агол)
тип	рамнинска фигура
образ	кружница
равенка	x²+y²=1
поддршка	центар=(0,0) полупречник=R=1
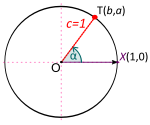
друго	аголот α=∠XOT е во стандардна позиција

Во геометријата, единична кружница е кружница со полупречник 1.^[1]^[2]^[3] Равенката на единична кружница со центар во координатниот почеток гласи $x^{2}+y^{2}=1$ . Единичната кружница помага при дефинирање на радијани (единица за мерење на агли) и при проширување на дефиницијата за тригонометриски вредности на било кој агол.

Единична кружница исто така е контурата (графиконот) на поларната функција ρ=1.
Единична кружница исто така е контурата (графиконот) на комплексната функција |z|=1, каде што |z| е модулот на z=x+iy.^[4]

Радијани и единичната кружница

Главните две единици за мерење на големина на агол се степени и радијани. Врската помеѓу овие единици е единичната кружница.^[5]

Имено, должината на периметарот на единична кружница е 2π≈6,2832.
Од друга страна, бројот на степени во цела кружница е 360°. Се дефинира 1 (радијан) да е 360°/_2π, т.е.

Единична кружница има периметар L=2π≈6,28

 $360^{\circ }=2\pi$    односно    $180^{\circ }=\pi \approx 3{,}1416$

Значи:

 $1={\frac {180^{\circ }}{\pi }}\approx 57{,}30^{\circ }$

Кај радијани не треба да се „пиши“ единица, туку само број. Честопати при првото објаснување на поимот радијани се пиши (радијани), но не треба. Ако големината на агол е дадена како број (би требало) да значи дека е зададена во радијани.^[6]

Регулатива: Доколку во математички израз или функција има некоја тригонометриски (или циклометриски) израз или функција, вредноста која се заменува (или се добива) мора да биде во радијани.

Пример: f(x)=x·sin(x). Пресметај f(2,17). Најпрво се проверува дека дигитронот е подесен во модот за радијани. Потоа f(2,17)= 2,17·sin(2,17)≈1,79

Пример: g(x)=–3·x·arctan(x). Пресметај g(2,17). Најпрво се проверува дека дигитронот е подесен во модот за радијани. Потоа g(2,17)= –3·2.17·arctan(2,17)≈= –7,41

Тригонометрија со единичната кружница

Стандардна позиција на агол

Во Декартов правоаголен координатен систем, агол α е во стандардна позиција ако темето е во О(0,0), почетниот крак е позитивниот дел од х-оска, а крајниот крак се добива по ротација за α и тоа:

Ако α≥0, т.е. ако α е позитивна, ротацијата е во насоката спротивна на стрелките на часовникот и
Ако α≤0, т.е. ако α е негативна, ротацијата е во насоката на стрелките на часовникот.

Понатаму, нека е даден било кој агол α (позитивна, негативна, голема, ...). Го цртаме аголот α во стандардна позиција во рамнината заедно со единичната кружница.

Точката T(b,a) нека е пресекот на крајната полуправа на аголот α со единична кружница.
Забелешка: Тука b е x-координатата, а a е y-координатата. Координатите, т.е. броевите b и a можат да бидат позитивни, негативни или нула во зависност од квадрантот во која лежи точката T. Меѓутоа:

 $a^{2}+b^{2}=1$

За точката Т(b,a) на единичната кружница, тригонометриските вредности на аголот α=∠XOT каде што X=(0,1) се:^[7]

 $\sin(\alpha )=a$   и   $\cos(\alpha )=b$   и   $\tan(\alpha )={\frac {a}{b}}$

Меѓуквадрантни агли

При агли кои завршуваат внатре во квадрантите, тригонометриски вредности се дефинираат преку референтни агли и референтните правоаголни триаголници (види тригонометрија). Тригонометриските вредности на агли кои завршуваат на еден од оските се пресметуваат преку единичната кружница. Референтните триаголници на овие агли се дегенерирани триаголници (се сплескуваат). Меѓутоа, координатите на нивната пресечна точка Т со единичната кружница едноставно се одредуваат само со гледање. На пример, точката Т за аголот 180° e пресекот на кружницата со негативниот дел од x-оската, т.е. T=(–1,0).


sin(0°)=0 cos(0°)=1 tan(0°)=0	sin(90°)=1 cos(90°)=0 tan(90°)= ∞	sin(180°)=0 cos(180°)= –1 tan(180°)=0	sin(270°)= –1 cos(270°)=0 tan(270°)= ∞

Се разбира дека овие формули важат и за сите агли котерминални со наведените агли.

Примери: Аголот 360° e котерминален со аголот 0°. Следува: sin(360°)=sin(0°)=0, cos(360°)=cos(0°)=1, tan(360°)=tan(0°)=0. Аголот –450° e котерминален со аголот 270°. Следува: sin(–450°)=sin(270°)=–1, cos(–450°)=cos(270°)=0, tan(–450°)=tan(270°)=∞.

Пресечната точка T на единичната кружница за агол α

Од друга страна, за одредување на пресечната точка Т на аголот α кој завршува внатре во квадрантите се користат тригонометриските вредности на α (види тригонометрија).

 $T(b,a)=T(\cos(\alpha ),\sin(\alpha ))$


$\sin(37^{\circ })\approx 0{,}6$ $\cos(37^{\circ })\approx 0{,}8$ $\tan(37^{\circ })\approx 0{,}75$	$\sin(217^{\circ })\approx -0{,}6$ $\cos(217^{\circ })\approx -0{,}8$ $\tan(217^{\circ })\approx 0{,}75$	$\sin(-53^{\circ })\approx -0{,}8$ $\cos(-53^{\circ })\approx 0{,}6$ $\tan(-53^{\circ })\approx -1{,}333$

Равенки на единичната кружница

Равенката на единичната кружница како реална функција y=f(x) од една реална променлива x е двозначна функција

f(x)=\pm {\sqrt {1-{x^{2}}}}

Равенката на единичната кружница како имплицитна зададена функција F(x,y)=C од две реални променливи x и y e

x^{2}+y^{2}=1

Равенката на единичната кружница како поларна функција ρ=ρ(φ) е константната функција, односно множеството на сите точки (ρ,φ) такви што ρ=1 (види поларни функции).

\rho (\phi )=1

Равенката на единичната кружница како комплексна функција z=z(x+iy) e множеството на сите комплексни броеви z=x+iy, такви што модулот на z e 1 (види комплексна функција).

\{z=x+iy\,\,{\boldsymbol {|}}\,\,|z|={\sqrt {x^{2}+y^{2}}}=1\}

Наводи

↑ Clapham, C.; Nicholson, J. (2009). „Oxford Concise Dictionary of Mathematics, Unit Circle“ (PDF) (англиски). Addison-Wesley. стр. 815. Посетено на 1 декември 2013.
↑ Pierce, Rod (2013). „Unit circle“ (англиски). Math is Fun. Посетено на 1 декември 2013.
↑ Staple, E. (2012). „Unit circle“ (англиски). Purple Math. Посетено на 1 декември 2013.
↑ Weisstein, Eric W. „Unit Circle“ (англиски). From MathWorld--A Wolfram Web Resource. Посетено на 1 декември 2013.
↑ „Radians“ (англиски). Math Open Reference. 2009. Посетено на 1 декември 2013. интерактивен
↑ „Are Angles Dimensionless?“ (англиски). Math Forum Drexel, Dr. Math. 2003. Посетено на 1 јануари 2014.
↑ Advanced Mathematical Concepts - Precalculus with Applications (англиски). Glencoe McGraw Hill. 2005. стр. 291. ISBN 978-0078682278.

Поврзано

Надворешни врски

Стојановска, Л. (2010). „Радијани“. Архивирано од изворникот на 2016-03-05. Посетено на 1 декември 2013. интерактивен
Стојановска, Л. (2010). „Помината пат по кружница“. Архивирано од изворникот на 2012-04-26. Посетено на 1 декември 2013. интерактивен
„Plotting Polar Functions“ (англиски). shoder.org. 2010. Посетено на 1 декември 2013. интерактивен

[Oxford-1] Clapham, C.; Nicholson, J. (2009). „Oxford Concise Dictionary of Mathematics, Unit Circle“ (PDF) (англиски). Addison-Wesley. стр. 815. Посетено на 1 декември 2013.

[2] Pierce, Rod (2013). „Unit circle“ (англиски). Math is Fun. Посетено на 1 декември 2013.

[3] Staple, E. (2012). „Unit circle“ (англиски). Purple Math. Посетено на 1 декември 2013.

[4] Weisstein, Eric W. „Unit Circle“ (англиски). From MathWorld--A Wolfram Web Resource. Посетено на 1 декември 2013.

[5] „Radians“ (англиски). Math Open Reference. 2009. Посетено на 1 декември 2013. интерактивен

[6] „Are Angles Dimensionless?“ (англиски). Math Forum Drexel, Dr. Math. 2003. Посетено на 1 јануари 2014.

[7] Advanced Mathematical Concepts - Precalculus with Applications (англиски). Glencoe McGraw Hill. 2005. стр. 291. ISBN 978-0078682278.

[1]

[2]

[3]

[4]

[5]

[6]

[7]