Бернулиева распределба
Бернулиева распределба во теоријата на веројатноста и статистиката — прекинатата веројатносна распределба на една случајна променлива која ја има вредноста 1 со веројатност и вредноста 0 со веројатност . Понеформално, таа е модел за множество можни исходи од секој можен опит опит кој поставува прашање „да–не“. Ваквите прашања водат до исходи со една од две вредности: „успех“ (1) со веројатност p и „неуспех“ (0) со веројатност q. Со оваа распределба може да се претстави фрлање паричка каде 1 и 0 би биле „глава“ и „писмо“, а p би била веројатноста да се падне глава (или обратно, каде 1 е писмо, а p ќе биде веројатноста за писмо). Нечесните парички би имале
|
Веројатносна функција 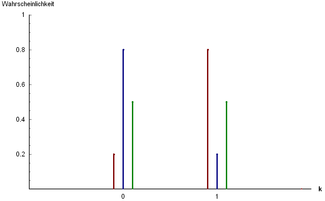
Три примери за Бернулиева распределба: и
и
и | |||
| Параметри |
| ||
|---|---|---|---|
| Носител | |||
| ВФ | |||
| РФ | |||
| Средина | |||
| Медијана | |||
| Модус | |||
| Варијанса | |||
| ПАО | |||
| Накосеност | |||
| Вишок зашиленост | |||
| Ентропија | |||
| МТФ | |||
| КФ | |||
| ВТФ | |||
| Фишерова информација | |||
Наречена е по швајцараскиот математичар Јакоб Бернули[1] и претставува посебен случај на биномната распределба со еден спроведен опит (така што n би бил 1 за таква биномна распределба). Воедно таа претставува посебен случај на двоточкестата распределба, чии можни исходи не мора да бидат 0 и 1.
Својства
уредиАко е случајна променлива со оваа распределба, тогаш:
Веројатносната фунција на оваа распределба низ можните исходи k е
Ова може да се изрази и како
или како
Бернулиевата распределба е посебен случај на биномната распределба со [3]
Зашиленоста оди до бесконечност за високи и ниски вредности на но за двоточкестите распределби (вкл. Бернулиевата) имаат помалку вишок зашиленост отколку било која друга веројатносна распределба, имено −2.
Бернулиевите распределби за сочинуваат експоненцијално семејство.
Процената на максимална веројатност на според случаен примерок е примерочната средина.
Средина
уредиОчекуваната вредност на една Бернулиева случајна променлива е
Ова се должи на тоа што, за Бернулиево распределена случајна променлива со и имаме
Веријанса
уредиВаријансата на Бернулиево распределен е
Прво имаме
Од ова следи
Од овој резултат лесно е да се докаже дека, за секоја Бернулиева распределба, нејзината варијанса ќе има вредност во рамките на .
Накосеност
уредиНакосеноста (коефициентот на асиметрија) е . Кога ја ќе земеме стандардизираната Бернулиево распределена случајна променлива излегува дека оваа случајна променлива добива со веројатност и добива со веројатност . Така добиваме
Виши моменти и кумуланти
уредиСите сирови моменти се еднакви поради тоа што и .
Централниот момент со степен се добива со
Првите шест централни моменти се
Вишите централни моменти може да се изразат покомпактно како и
Првите шест кумуланти се
Поврзани распределби
уреди- Ако се независни еднакво распределени случајни променливи, сите Бернулиеви опити со веројатност за успех p, тогаш нивното множество е распределено според биномна распределба со параметри n и p:
- (биномна распределба).[2]
- Бернулиевата распределба едноставно е , и се запишува и како
- Категоричната распределба е воопштувањето на Бернулиевата распределба за променливи со било кој постојан број на прекинати вредности.
- Бета-распределбата е сврзувачкиот претходник of Бернулиевата распределба.
- Геометриската распределба го моделира бројот на независни и еднакви Бернулиеви опити потребни за да се добие еден успех.
- Ако , тогаш има Радемахерова распределба.
Поврзано
уредиНаводи
уреди- ↑ James Victor Uspensky: Introduction to Mathematical Probability, McGraw-Hill, New York 1937, стр. 45
- ↑ 2,0 2,1 2,2 2,3 Bertsekas, Dimitri P. (2002). Introduction to Probability. Tsitsiklis, John N., Τσιτσικλής, Γιάννης Ν. Belmont, Mass.: Athena Scientific. ISBN 188652940X. OCLC 51441829.
- ↑ McCullagh, Peter; Nelder, John (1989). Generalized Linear Models, Second Edition. Boca Raton: Chapman and Hall/CRC. Section 4.2.2. ISBN 0-412-31760-5.
Надворешни врски
уреди| „Бернулиева распределба“ на Ризницата ? |
- Хацевинкел, Михил, уред. (2001), „Биномна распределба“, Математичка енциклопедија, Шпрингер, ISBN 978-1556080104.
- „Бернулиева распределба“ од Ерик В. Вајсштајн — MathWorld (англиски)













![{\displaystyle {\begin{cases}0&{\text{ако }}p<1/2\\\left[0,1\right]&{\text{ако }}p=1/2\\1&{\text{ако }}p>1/2\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2653cf6608e09c52e4f9c5aeef62bcf0eef39fde)









