Празно множество

Празно множество – во математиката и нејзината област теорија на множествата е единствено множество кое не содржи елементи. Во аксиоматската теорија на множествата, постоењето на празното множество е постулирано со аксиомата на празно множество.

Празното множество е множество кое не содржи елементи

Обележување

Симбол за празното множество

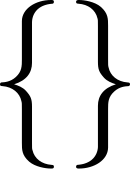
Празното множество се означува со симболот $\varnothing$ или $\emptyset$ што доаѓа од буквата Ø од данската и норвешката абецеда. Симболот го вовела групата Бурбаки (конкретно Андре Вејл) во 1939 година. Исто така празното множество се обележува и со {}.

Својства

Во теоријата на множества, две множества се еднакви ако имаат исти елементи, според тоа може да постои само едно множество без елементи. Значи постои само едно празно множество, па зборуваме за „празното множество“, а не за „празно множество“.

За кое било множество A

• празното множество е подмножество од A:

  ∀A: ∅ ⊆ A

• унија на A и празно множество е еднаква на A:

  ∀A: A ∪ ∅ = A

• За секое множество A, пресек на A и празно множество е празно множество:

  ∀A: A ∩ ∅ = ∅

• За секое множество A, Декартов производ на A и празно множество е празен:

  ∀A: A × ∅ = ∅

Празното множество ги има следниве својства:

• Единствено подмножество на празното множество е самото празно множество:

  ∀A: A ⊆ ∅ ⇒ A = ∅

• Партитивно множество на празното множество е множеството кое го содржи само празното множество:

  $2^{\emptyset }=\{\emptyset \}$

• Бројот на елементи на празното множество (т.е. неговата кардиналност) е нула; празното множество е конечно множество:

  |∅| = 0

За кое било својство:

• за секој елемент од ∅ својството важи
• не постои елемент од ∅ за кој својството важи

Обратно: ако за некое својство важат следниве две тврдења:

• за секој елемент V својство важи
• не постои елемент V за кој својство важи

тогаш V = ∅

Надворешни врски

• „Empty Set“ од Ерик В. Вајсштајн — MathWorld (англиски)