Дифракција (скршнување или свиткување) — различни појави кои се јавуваат кога еден бран наидува на пречка или процеп. Таа е дефинирана како свиткување на брановите околу аглите на пречката или отворот во регионот на геометриската сенка на пречката. Во класичната физика, појавата на дифракција е опишан како мешање на брановите според принципот на Хајгенс-Френеловиот закон кој ја третира секоја точка во брановите предници како збирка од поединечни сферични бранови.^[1] Овие карактеристични однесувања се изложени кога еден бран се соочува со пречка или процеп што е споредлив со големината на нејзината бранова должина. Слични ефекти се јавуваат кога светлосниот бран патува низ медиум со различен показател на прекршување или кога звучниот бран патува низ медиум со различна акустична импеданса. Дифракцијата има влијание врз акустичниот простор. Дифракцијата се јавува кај сите бранови, вклучувајќи звучни бранови, водени бранови и електромагнетни бранови како видлива светлина, Х-зраци и радио бранови.

Уште пред физичките објекти да имаат брановидни својства (на атомско ниво), дифракцијата се јавува и со материјата и може да се изучува според принципите на квантната механика. Италијанскиот научник Франческо Марија Грималди кој го измислил зборот "дифракција" и бил прв кој ги снимил точните набљудувања на оваа појава во 1660 година.^[2]^[3]

Додека дифракцијата се јавува кога патувачките бранови наидуваат на вакви промени, нејзините ефекти обично се најизразени за брановите чија бранова должина е грубо споредлива со димензиите на дифракцискиот објект или процепот. Доколку опструирачкиот објект обезбедува повеќекратно, тесно распоредени отвори и може да резултира со комплексен модел со различен интензитет ова се должи на додавање или мешање на различни делови на бранот кои патуваат до набљудувачот со различни патеки, каде што различните должини на патеката резултираат со различни фази. Формализмот на дифракцијата, исто така, може да го опише начинот на кој брановите на конечна мера се шират во слободен простор. На пример, проширувачкиот профил на ласерски зрак, обликот на радарот на радарска антена и полето на гледање на ултразвукови трансдуцери, сите може да се анализираат користејќи дифракциони равенки.

Примери

Ефектите на дифракцијата често се гледаат во секојдневниот живот. Највпечатливи примери на дифракција се оние кои вклучуваат светлина. На пример, тесно распоредените песни на ЦД или ДВД дејствуваат како дифракционен хелиум за да се формира позната шема на виножито која се гледа кога гледаме на диск. Овој принцип може да се прошири за да се изработи хелиум со структура со тоа што ќе произведе посакуван образец на дифракција; Холограмот на кредитна картичка е пример. Дифракцијата во атмосферата со мали честички може да предизвика светол прстен кој ќе биде видлив околу изворот на светлина, како што е сонцето или месечината. Сенка на цврст објект, користејќи светлина од компактен извор, покажува мали реси во близина на неговите рабови. Светкавиот дезен кој се забележува кога ласерската светлина паѓа на оптички груба површина е исто така дифракциона појава. Кога месото е извонредно, тоа е дифракција од месните влакна.^[4] Сите овие ефекти се последица на фактот дека светлината се движи како бран.

Дифракцијата може да се случи со каков било бран. Океанските бранови дифракцираат околу дамки и други пречки. Звучните бранови можат да се разликуваат околу предметите, поради што сè уште може да се слушне некој повик дури и кога се крие зад дрвото.^[5] Дифракцијата, исто така, може да биде проблем во некои технички апликации, таа поставува основно ограничување на резолуцијата на камера, телескоп или микроскоп.

Историја

Ефектите од дифракцијата на светлината првично биле внимателно набљудувани и карактеризирани од Франческо Марија Грималди, кој исто така го измислил дифракциониот поим од латинската фраза "да се пробие на парчиња", осврнувајќи се на светлината што паѓа во различни правци. Резултатите од набљудувањата на Грималди беа објавени во 1665 година.^[6]^[7]^[8] Исак Њутн ги проучувал овие ефекти и ги препишувал на рефлексијата на светлосни зраци. Џејмс Грегори (1638-1675) ги набљудувал шаблоните на дифракција предизвикани од пердув од птици. Така била откриена првата дифракциона решетка.^[9] Томас Јунг извел прославен експеримент во 1803 година, демонстрирајќи мешање од две тесно распоредени пресеци.^[10] Објаснувајќи ги неговите резултати со мешање на брановите кои произлегуваат од двата различни пресеци, тој дознал дека светлината се шири како бранови. Огистен-Жан Френел направил повеќе конечни студии и пресметки за дифракција, објавени во 1815^[11] и 1818^[12] година, и на тој начин дал голема поддршка на брановата теорија на светлина, која била развиена од страна на Кристијан Хајгенс^[13] и обновена од Јунг која била против Њутновата теорија на честички.

Механизам

Во традиционалната класична физика се јавува дифракција поради начинот на кој брановите се шират; ова е опишано со принципот на Хајгенс-Френел и принципот на суперпозиција на бранови. Проширувањето на бранот може да се визуелизира со разгледување на секоја честичка на пренесената средина на бранот како извор за секундарен сферичен бран. Движењето на бран во која било точка е збирот на овие секундарни бранови. Кога брановите се собираат заедно, нивната сума се определува со релативните фази, како и со амплитудите на поединечните бранови, така што сумираната амплитуда на брановите може да има било која вредност помеѓу нула и збирот на поединечните амплитуди. Оттука, шаблоните на дифракција обично имаат серија на максими и минимум. Во современото квантно механичко разбирање на размножувањето на светлината преку решетка (или прореза), секој фотон го има она што е познато како бранова функција која го опишува својот пат од извор преку процепот до екранот. Брановата функција (патеката што ќе ја има фотонот) е одредена од физичката околина како што е геометријата на процепот, оддалеченоста на екранот и почетните услови кога се создава фотон. Во важни експерименти (опит со два процепа со низок интензитет првпат го изврши Г. И. Тејлор во 1909 година) беше демонстрирано постоењето на брановата функција на фотонот. Преку квантниот пристап дифракцискиот модел е создаден со дистрибуција на патеки, набљудувањето на светлината и темните ленти е присуството или отсуството на фотони во овие области (без интерференција). Квантниот пристап има некои впечатливи сличности со принципот на Хајгенс-Френеловиот принцип, во тој принцип светлината станува серија на поединечно распределени светлосни извори низ цевката што е слична на ограничен број на патеки (или функции на бранови) достапни за фотоните да патуваат преку решетката. Постојат различни аналитички модели кои овозможуваат пресметување на дифракциони полиња, вклучувајќи ја и дифракциската равенка на Кирхоф и Френел која е изведена од бранова равенка, Фраунхофер дифракциска аппроксимација на Кирхофовата равенка која се применува на далеку полето и апсорпцијата на Френел дифракција која се применува на блиското поле. Повеќето конфигурации не можат да се решат аналитички, но можат да дадат бројчени решенија преку методот на конечни елементи и гранични елементи. Можно е да се добие квалитативно разбирање на многу дифракциони појави со оглед на тоа како релативните фази на поединечните извори на вториот бран кои варираат, а особено условите во кои фазната разлика е еднаква на половина циклус, каде во тој случај брановите ќе ги снема. Наједноставните описи на дифракцијата се оние во кои ситуацијата може да се сведе на дводимензионален проблем. За водени бранови, тие се шират само на површината на водата. За светлина, често може да се занемари една насока ако дифракцискиот објект се протега во таа насока на далечина далеку поголемо од брановата должина. Во случај на светлина која сјае низ мали кружни дупки, ќе треба да ја земеме предвид целосната тридимензионална природа на проблемот.

Фотографија од дифракција низ препрека со еден отвор во кружна бранова када.

Дифракција на светлината

Некои примери за дифракцијата на светлината се дадени подолу.

Дифракција низ еден отвор

Дифракција на ЦД и ДВД.

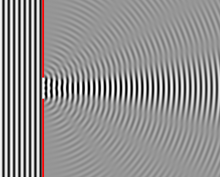
Долга решетка од бесконечна ширина која е осветлена со светлина ја дифрактира светлината во серија на кружни бранови, а бранот кој излегува од процепот е цилиндричен бран со униформен интензитет.Решетката што е поширока од бранова должина создава ефекти на интерференција во просторот од процепот. Овие можат да се објаснат под претпоставка дека пределот се однесува како да има голем број точни извори распоредени рамномерно низ ширината на процепот. Анализата на овој систем е поедноставена ако ја земеме предвид светлината на една бранова должина. Ако упадното светло е кохерентно, овие извори ја имаат истата фаза. Упадот на светлината во одредена точка во просторот низ процепот е составен од придонеси од секој од овие точни извори и релативните фази на овие придонеси се разликуваат за 2π или повеќе, може да очекуваме да пронајдеме минимум и максимум во дифракционата светлина . Ваквите фазни разлики се предизвикани од разлики во должината на патеката преку која придонесувачките зраци стигнуваат до точка од отворот.

Ние можеме да го најдеме аголот на кој се добива првиот минимум во дифрагираната светлина со следните размислувања. Светлината од извор кој се наоѓа на горниот раб на процепот, деструктивно се меша со извор кој се наоѓа на средината на процепот, кога разликата во патот помеѓу нив е еднаква на λ/2. Слично на тоа, изворот веднаш под врвот на процепот ќе се меша деструктивно со изворот кој се наоѓа веднаш под средината на процепот под ист агол. Ние можеме да го продолжиме ова размислување по должината на целата висина на процепот за да заклучиме дека условот за деструктивна интерференца за целиот процеп е ист како условот за деструктивна интерференција помеѓу два тесни отвори на растојание што е половина од ширината на процепот. Разликата во патеката е приближно ${\frac {d\sin(\theta )}{2}}$ така што минималниот интензитет дејствува под агол θ_min даден од

d\,\sin \theta _{\text{min}}=\lambda

.

каде:

d е ширина на отворот,
$\theta _{\text{min}}$ е упадниот агол при кој настанува минимумот
$\lambda$ е брановата должина на светлината.

Сличен аргумент може да се користи за да се покаже дека ако замислиме дека процепот треба да се подели на четири, шест, осум делови, итн, минимите се добиваат под агли θn дадени од

d\,\sin \theta _{n}=n\lambda

каде

n е цел број различен од нула.

Не постои таков едноставен аргумент кој ни овозможува да го најдеме максимумот на дифракционата шема. Профилот на интензитет може да се пресмета со помош на дифракциската равенка на Фраунхофер како

I(\theta )=I_{0}\,\operatorname {sinc} ^{2}\left({\frac {d\pi }{\lambda }}\sin \theta \right)

каде

$I(\theta )$ е јачината при одреден агол,
$I_{0}$ е првичната јачина, и
Синусната функција од погоре е определена $\operatorname {sinc} (x)={\frac {\sin x}{x}}$ ако $x\neq 0$ , и $\operatorname {sinc} (0)=1$

Оваа анализа се однесува само на крајното поле, односно на растојание многу поголемо од ширината на процепот.

Дифракција на црвен ласер низ 2 отвори (горе) и 5 отвори.

Дифракциона решетка

Дифракциона решетка/мрежичка.

Дифракциона решетка е оптичка компонента со непроменлив шаблон. Обликот на светлината дифрацирани низ дифракциона решетка зависи од структурата на елементите и бројаот на присутни елементи, но сите решетки максимална јачина при агли θ_m кои се дадени со равенката за дифракциона решетка

d\left(\sin {\theta _{m}}+\sin {\theta _{i}}\right)=m\lambda .

каде

θ_i е аголот на упадната светлина,
d е растојанието меѓу отворите на решетката, и
m е цел број кој може да биде позитивен или негативен.

Светлината дифркацирана од страна на хелиум се наоѓа со сумирање на светлината од секој од елементите, и во суштина е склоност на дифракција и интерферентни шеми.На сликата е прикажано дифракцирано светло од 2-елемент и 5-елемент решетки, каде може да се види дека максимумот е во иста положба, но деталните структури на интензитетите се различни.

Сметачки создадена слика на **Ејриев диск**.

Кружен отвор

Надворешната дифракција на авионскиот бран инцидентен на кружен отвор често се нарекува Воздушен диск. Вариацијата на интензитетот со агол е дадена со

I(\theta )=I_{0}\left({\frac {2J_{1}(ka\sin \theta )}{ka\sin \theta }}\right)^{2}

,

каде што a е полупречникот на кружниот отвор, k е еднакво на 2π/λ и J₁ е Беселовата функција. Колку е помала решетката, толку е поголема големината на самото место на одредено растојание, и колку е поголема дивергенцијата на дифракционираните зраци.

Општа решетка

Бран што произлегува од точен извор има амплитуда Ѱ на локацијата r која е дадена со решението на честотната бранова равенка за точен извор (равенката Хелмхолц)

\nabla ^{2}\psi +k^{2}\psi =\delta (\mathbf {r} )

каде $\delta (\mathbf {r} )$ е 3-димензионална делта функција. Функцијата на делта има само радијална зависност, така што операторот Лаплас (a.k.a. скаларен лапласијан) во сферичниот координатен систем се поедноставува (види дел во цилиндрични и сферични координати)

\nabla ^{2}\psi ={\frac {1}{r}}{\frac {\partial ^{2}}{\partial r^{2}}}(r\psi )

Со директна замена, решението за оваа равенка може лесно да се прикаже како скаларна функција на Грина, која во сферичниот координатен систем (и со користење на физичката временска конвенција)

\psi (r)={\frac {e^{ikr}}{4\pi r}}

Ова решение претпоставува дека изворот на делта функција се наоѓа на потекло. Ако изворот се наоѓа на произволна изворна точка, означена со векторот и полето на полето се наоѓа на точката, тогаш можеме да ја претставуваме функцијата на скаларната Грина (за произволна изворна локација) како: Затоа, ако електричното поле е инцидент на екранот, полето произведено со оваа апертурна дистрибуција е дадено од површинскиот интеграл: За пресметка на полињата Fraunhofer регионоткаде што изворот точка во отвор е даден од векторот

\psi (\mathbf {r} |\mathbf {r} ')={\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{4\pi |\mathbf {r} -\mathbf {r} '|}}

Следствено, iако електричното поле, E_inc(x,y) е упадно во отворот, полето создадено од отворотраспределбата се определува со површинскиот интеграл:

\Psi (r)\propto \iint \limits _{\mathrm {aperture} }E_{\mathrm {inc} }(x',y')~{\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{4\pi |\mathbf {r} -\mathbf {r} '|}}\,dx'\,dy',

За преметување на полињата во Фраунхоферовата област.

каде точката на изворот во отворот е дадена со векторот

\mathbf {r} '=x'\mathbf {\hat {x}} +y'\mathbf {\hat {y}}

Во далечното поле, каде може да се искористи приближноста за параллелни зраци, односно Гриновата функција,

\psi (\mathbf {r} |\mathbf {r} ')={\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{4\pi |\mathbf {r} -\mathbf {r} '|}}

се упростува на

\psi (\mathbf {r} |\mathbf {r} ')={\frac {e^{ikr}}{4\pi r}}e^{-ik(\mathbf {r} '\cdot \mathbf {\hat {r}} )}

како што може да се види на сликата десно (Приотиснете за да ја зголемите).

Изразот за полето во далечната област (Фраунхоферовата област) станува

\Psi (r)\propto {\frac {e^{ikr}}{4\pi r}}\iint \limits _{\mathrm {aperture} }E_{\mathrm {inc} }(x',y')e^{-ik(\mathbf {r} '\cdot \mathbf {\hat {r}} )}\,dx'\,dy',

Сега, бидејќи

\mathbf {r} '=x'\mathbf {\hat {x}} +y'\mathbf {\hat {y}}

и

\mathbf {\hat {r}} =\sin \theta \cos \phi \mathbf {\hat {x}} +\sin \theta ~\sin \phi ~\mathbf {\hat {y}} +\cos \theta \mathbf {\hat {z}}

изразот за полето во Фраунхоферовата област за планарниот отвор сега станува,

\Psi (r)\propto {\frac {e^{ikr}}{4\pi r}}\iint \limits _{\mathrm {aperture} }E_{\mathrm {inc} }(x',y')e^{-ik\sin \theta (\cos \phi x'+\sin \phi y')}\,dx'\,dy'

Допуштајќи,

k_{x}=k\sin \theta \cos \phi \,\!

и

k_{y}=k\sin \theta \sin \phi \,\!

полето во Фраунхоферовата област на планарниот отвор го добива обликот на Фуриевата трансформација

\Psi (r)\propto {\frac {e^{ikr}}{4\pi r}}\iint \limits _{\mathrm {aperture} }E_{\mathrm {inc} }(x',y')e^{-i(k_{x}x'+k_{y}y')}\,dx'\,dy',

Во далечното поле / Фраунхоферовата област, се добива просторната Фуриева трансформација на распределбата од отворот. Кога ќе се примени Хајгенсовиот принцип на отворот вели дела шаблонот на полето при далечна дифракција е просторна Фуриева трансформација на обликот на отворот, и ова е директен дополнителен производ од користењето на приближноста на паралелни зраци, што пак е слично на разложувањето на рамнински бран на рамнински полиња низ отворот (Погледајте Фуриева оптика).

Модели

Аголното растојание на функциите во дифракциона шема е обратно пропорционално со димензиите на објектот што ја предизвикува дифракцијата. Со други зборови: Помалиот дифракциски објект, "пошироката" добиена дифракциона шема и обратно. (Попрецизно, ова е точно за синусите на аглите.)

Дифракционите агли се инвариантни при скалирање; тоа значи дека тие зависат само од односот на брановата должина до големината на дифракцискиот објект.

Кога дифракцискиот објект има периодична структура, на пример во дифракциона хелиум, функциите обично стануваат поостри. Третата фигура, на пример, покажува споредба на двојна пресечна шема со модел формиран од пет пресеци, и двете групи на пресеци кои имаат ист простор, помеѓу центарот на еден процеп и наредната.

Честична дифракција

Квантната теорија ни кажува дека секоја честичка покажува својства на бран. Особено, масивните честички можат да се мешаат и да се добие дифракција. Дифракцијата на електрони и неутрони стои како еден од моќните аргументи во корист на квантната механика. Брановидна должина поврзана со честичка се нарекува де Броголивата бранова должина и се означува

каде h е Планкова константа и p е имплус на честитчка (маса ×брзина за бавни честички).

За повеќето макроскопски објекти, оваа бранова должина е толку кратка што не е значајно да им се додели бранова должина на нив. Атриум на натриум кој патувал на околу 30.000 м/с би имал брановата должина од Броголивата бранова дплжина од околу 50 пикометри.

Бидејќи бранова должина за дури и најмалите макроскопски објекти е исклучително мала, дифракцијата на материјалните бранови е видлива само за мали честички, како што се електроните, неутроните, атомите и малите молекули. Кратката бранова должина на овие материјални бранови ги прави идеално погодни за проучување на атомската кристална структура на цврсти материи и големите молекули како белковини.

Релативно поголеми молекули како buckyballs, исто така, можат да дифракцираат.

Брег дифракција

Дифракцијата од тридимензионална периодична структура, како што се атомите во кристал, се нарекува Брег дифракција. Тоа е слично на она што се случува кога брановите се расфрлани од дифракционен хелиум. Брег дифракцијата е последица на интерференција помеѓу брановите што се рефлектираат од различни кристални рамнини. Состојбата на конструктивните пречки е дадена со Брегговиот закон

каде

λ е брановата должина, d е растојанието помеѓу кристалните рамнини, θ е аголот на дифрагираниот бран и m е цел број познат како редослед на дифракцискиот сноп.

Брег дифракцијата може да се изврши со помош на светлина со многу кратка бранова должина како Х-зраците или материјални бранови како неутрони (и електрони), чија бранова должина е по ред (или многу помала од) атомското растојание. Произведениот образец дава информации за одделувањата на кристалографските рамнини d, овозможувајќи да се заклучи кристалната структура. Контраст на дифракција, особено кај електронските микроскопи и уредите со x-топографија, е моќна алатка за испитување на поединечни дефекти и локални полиња во кристали.

Поврзано

Наводи

↑ Wireless Communications: Principles and Practice, Prentice Hall communications engineering and emerging technologies series, T. S. Rappaport, Prentice Hall, 2002 pg 126
↑ Francesco Maria Grimaldi, Physico mathesis de lumine, coloribus, et iride, aliisque annexis libri duo (Bologna ("Bonomia"), Italy: Vittorio Bonati, 1665), page 2 Архивирано на 1 декември 2016 г.:
Original : Nobis alius quartus modus illuxit, quem nunc proponimus, vocamusque; diffractionem, quia advertimus lumen aliquando diffringi, hoc est partes eius multiplici dissectione separatas per idem tamen medium in diversa ulterius procedere, eo modo, quem mox declarabimus.

Translation : It has illuminated for us another, fourth way, which we now make known and call "diffraction" [i.e., shattering], because we sometimes observe light break up; that is, that parts of the compound [i.e., the beam of light], separated by division, advance farther through the medium but in different [directions], as we will soon show.
↑ Cajori, Florian "A History of Physics in its Elementary Branches, including the evolution of physical laboratories." Архивирано на 1 декември 2016 г. MacMillan Company, New York 1899
↑ Arumugam, Nadia. „Food Explainer: Why Is Some Deli Meat Iridescent?“. Slate. The Slate Group. Архивирано од изворникот на 10 September 2013. Посетено на 9 September 2013.
↑ Andrew Norton (2000). Dynamic fields and waves of physics. CRC Press. стр. 102. ISBN 978-0-7503-0719-2.
↑ Francesco Maria Grimaldi, Physico-mathesis de lumine, coloribus, et iride, aliisque adnexis … [The physical mathematics of light, color, and the rainbow, and other things appended …] (Bologna ("Bonomia"), (Italy): Vittorio Bonati, 1665), pp. 1–11 Архивирано на 1 декември 2016 г.: "Propositio I. Lumen propagatur seu diffunditur non solum directe, refracte, ac reflexe, sed etiam alio quodam quarto modo, diffracte." (Proposition 1. Light propagates or spreads not only in a straight line, by refraction, and by reflection, but also by a somewhat different fourth way: by diffraction.) On p. 187, Grimaldi also discusses the interference of light from two sources: "Propositio XXII. Lumen aliquando per sui communicationem reddit obscuriorem superficiem corporis aliunde, ac prius illustratam." (Proposition 22. Sometimes light, as a result of its transmission, renders dark a body's surface, [which had been] previously illuminated by another [source].)
↑ Jean Louis Aubert (1760). Memoires pour l'histoire des sciences et des beaux arts. Paris: Impr. de S. A. S.; Chez E. Ganeau. стр. 149.
↑ Sir David Brewster (1831). A Treatise on Optics. London: Longman, Rees, Orme, Brown & Green and John Taylor. стр. 95. Архивирано од изворникот на 2016-12-01.
↑ Letter from James Gregory to John Collins, dated 13 May 1673. Reprinted in: Correspondence of Scientific Men of the Seventeenth Century …, ed. Stephen Jordan Rigaud (Oxford, England: Oxford University Press, 1841), vol. 2, pp. 251–255, especially p. 254 Архивирано на 1 декември 2016 г..
↑ Thomas Young (1804-01-01). „The Bakerian Lecture: Experiments and calculations relative to physical optics“. Philosophical Transactions of the Royal Society of London. 94: 1–16. doi:10.1098/rstl.1804.0001.. (Note: This lecture was presented before the Royal Society on 24 November 1803.)
↑ Augustin-Jean Fresnel (1816) "Mémoire sur la Diffraction de la lumière, où l'on examine particulièrement le phénomène des franges colorées que présentent les ombres des corps éclairés par un point lumineux" (Memoir on the diffraction of light, in which is examined particularly the phenomenon of colored fringes that the shadows of bodies illuminated by a point source display), Annales de la Chimie et de Physique, 2nd series, vol. 1, pages 239–281. (Presented before l'Académie des sciences on 15 October 1815.)
↑
See:
- Excerpts from Fresnel's paper on diffraction were published in 1819: A. Fresnel (1819) "Mémoire sur la diffraction de la lumière" (Memoir on the diffraction of light), Annales de chimie et de physique, 11 : 246–296 Архивирано на 1 декември 2016 г. and 337–378. Архивирано на 1 декември 2016 г.
- The complete version of Fresnel's paper on diffraction was published in 1821: Augustin-Jean Fresnel (1821) "Mémoire sur la diffraction de la lumière" Архивирано на 7 септември 2014 г. (Memoir on the diffraction of light), Mémoires de l'Académie des sciences de l'Institut de France, 5 : 339–475. (Summitted to l'Académie des sciences of Paris on 20 April 1818.)
↑ Christiaan Huygens, Traité de la lumiere … Архивирано на 16 јуни 2016 г. (Leiden, Netherlands: Pieter van der Aa, 1690), Chapter 1. From p. 15 Архивирано на 1 декември 2016 г.: "J'ay donc monstré de quelle façon l'on peut concevoir que la lumiere s'etend successivement par des ondes spheriques, … " (I have thus shown in what manner one can imagine that light propagates successively by spherical waves, … ) (Note: Huygens published his Treatise on Light in 1690; however, in the preface to his book, Huygens states that in 1678 he first communicated his book to the French Royal Academy of Sciences.)

Надворешни врски

[1] Wireless Communications: Principles and Practice, Prentice Hall communications engineering and emerging technologies series, T. S. Rappaport, Prentice Hall, 2002 pg 126

[2] Francesco Maria Grimaldi, Physico mathesis de lumine, coloribus, et iride, aliisque annexis libri duo (Bologna ("Bonomia"), Italy: Vittorio Bonati, 1665), page 2 Архивирано на 1 декември 2016 г.:
Original : Nobis alius quartus modus illuxit, quem nunc proponimus, vocamusque; diffractionem, quia advertimus lumen aliquando diffringi, hoc est partes eius multiplici dissectione separatas per idem tamen medium in diversa ulterius procedere, eo modo, quem mox declarabimus.

Translation : It has illuminated for us another, fourth way, which we now make known and call "diffraction" [i.e., shattering], because we sometimes observe light break up; that is, that parts of the compound [i.e., the beam of light], separated by division, advance farther through the medium but in different [directions], as we will soon show.

[3] Cajori, Florian "A History of Physics in its Elementary Branches, including the evolution of physical laboratories." Архивирано на 1 декември 2016 г. MacMillan Company, New York 1899

[4] Arumugam, Nadia. „Food Explainer: Why Is Some Deli Meat Iridescent?“. Slate. The Slate Group. Архивирано од изворникот на 10 September 2013. Посетено на 9 September 2013.

[5] Andrew Norton (2000). Dynamic fields and waves of physics. CRC Press. стр. 102. ISBN 978-0-7503-0719-2.

[6] Francesco Maria Grimaldi, Physico-mathesis de lumine, coloribus, et iride, aliisque adnexis … [The physical mathematics of light, color, and the rainbow, and other things appended …] (Bologna ("Bonomia"), (Italy): Vittorio Bonati, 1665), pp. 1–11 Архивирано на 1 декември 2016 г.: "Propositio I. Lumen propagatur seu diffunditur non solum directe, refracte, ac reflexe, sed etiam alio quodam quarto modo, diffracte." (Proposition 1. Light propagates or spreads not only in a straight line, by refraction, and by reflection, but also by a somewhat different fourth way: by diffraction.) On p. 187, Grimaldi also discusses the interference of light from two sources: "Propositio XXII. Lumen aliquando per sui communicationem reddit obscuriorem superficiem corporis aliunde, ac prius illustratam." (Proposition 22. Sometimes light, as a result of its transmission, renders dark a body's surface, [which had been] previously illuminated by another [source].)

[7] Jean Louis Aubert (1760). Memoires pour l'histoire des sciences et des beaux arts. Paris: Impr. de S. A. S.; Chez E. Ganeau. стр. 149.

[8] Sir David Brewster (1831). A Treatise on Optics. London: Longman, Rees, Orme, Brown & Green and John Taylor. стр. 95. Архивирано од изворникот на 2016-12-01.

[9] Letter from James Gregory to John Collins, dated 13 May 1673. Reprinted in: Correspondence of Scientific Men of the Seventeenth Century …, ed. Stephen Jordan Rigaud (Oxford, England: Oxford University Press, 1841), vol. 2, pp. 251–255, especially p. 254 Архивирано на 1 декември 2016 г..

[10] Thomas Young (1804-01-01). „The Bakerian Lecture: Experiments and calculations relative to physical optics“. Philosophical Transactions of the Royal Society of London. 94: 1–16. doi:10.1098/rstl.1804.0001.. (Note: This lecture was presented before the Royal Society on 24 November 1803.)

[11] Augustin-Jean Fresnel (1816) "Mémoire sur la Diffraction de la lumière, où l'on examine particulièrement le phénomène des franges colorées que présentent les ombres des corps éclairés par un point lumineux" (Memoir on the diffraction of light, in which is examined particularly the phenomenon of colored fringes that the shadows of bodies illuminated by a point source display), Annales de la Chimie et de Physique, 2nd series, vol. 1, pages 239–281. (Presented before l'Académie des sciences on 15 October 1815.)

[12] See:
Excerpts from Fresnel's paper on diffraction were published in 1819: A. Fresnel (1819) "Mémoire sur la diffraction de la lumière" (Memoir on the diffraction of light), Annales de chimie et de physique, 11 : 246–296 Архивирано на 1 декември 2016 г. and 337–378. Архивирано на 1 декември 2016 г.

The complete version of Fresnel's paper on diffraction was published in 1821: Augustin-Jean Fresnel (1821) "Mémoire sur la diffraction de la lumière" Архивирано на 7 септември 2014 г. (Memoir on the diffraction of light), Mémoires de l'Académie des sciences de l'Institut de France, 5 : 339–475. (Summitted to l'Académie des sciences of Paris on 20 April 1818.)

[13] Excerpts from Fresnel's paper on diffraction were published in 1819: A. Fresnel (1819) "Mémoire sur la diffraction de la lumière" (Memoir on the diffraction of light), Annales de chimie et de physique, 11 : 246–296 Архивирано на 1 декември 2016 г. and 337–378. Архивирано на 1 декември 2016 г.

[14] The complete version of Fresnel's paper on diffraction was published in 1821: Augustin-Jean Fresnel (1821) "Mémoire sur la diffraction de la lumière" Архивирано на 7 септември 2014 г. (Memoir on the diffraction of light), Mémoires de l'Académie des sciences de l'Institut de France, 5 : 339–475. (Summitted to l'Académie des sciences of Paris on 20 April 1818.)

[13] Christiaan Huygens, Traité de la lumiere … Архивирано на 16 јуни 2016 г. (Leiden, Netherlands: Pieter van der Aa, 1690), Chapter 1. From p. 15 Архивирано на 1 декември 2016 г.: "J'ay donc monstré de quelle façon l'on peut concevoir que la lumiere s'etend successivement par des ondes spheriques, … " (I have thus shown in what manner one can imagine that light propagates successively by spherical waves, … ) (Note: Huygens published his Treatise on Light in 1690; however, in the preface to his book, Huygens states that in 1678 he first communicated his book to the French Royal Academy of Sciences.)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]