Четиридимензионален простор
Концептот за четврта димензија (кратенка: 4Д) често се опишува со оглед на неговите физички импликации; т.е. знаеме дека во три димензии, имаме должина (или длабочина), широчина и висина. Четвртата димензија е ортогонална (под прав агол) на трите други просторни димензии. Главните насоки на трите познати димензии се наречени горна/долна (височина), северна/јужна(должина) и источна/западна (ширина). Кога зборуваме за четвртата димензија, потребен е додатен пар од изрази. Прифатени изрази се ана/ката, вин/вут (користена од Руди Рукер) и ипсилон/делта.
Обично четвртата димензија се поистоветува со време. Во овој случај, концептот на додатна просторна димензија би се нарекол петта димензија.
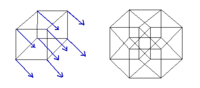
Концепти
уредиВекторски простори
уредиВекторски простор е множество вектори, кои можеме да ги замислиме како стрелки, со заедничка појдовна точка во просторот наречена зачеток (геометриски вектори), а таа точка пак лежи на други места во просторот. Да ги погледаме следниве интуитивни концепти за да можеме да изградиме дефиниција за димензија.
Точката е бездимензионален објект. Таа воопшто не се протега во просторот, и нема никакви својства. Ако оваа точка би ја сметале за геометриски вектор, како стрелка, таа не би имала должина. Овој вектор се нарекува нулти вектор и, сам по себе, е најпростиот векторски простор.
Линијата е еднодимензионален објект. Ако земеме некој (ненулски) вектор во просторот, тој ќе има конечна должина. Тој вектор има глава некаде во просторот и опашка при неговиот зачеток. Ако го растегнеме векторот за да го издолжиме двојно, тројно, и така што го издолжуваме наназад така што ќе ги има сите можни должини (дури и нулта должина, за да го добиеме нултиот вектор), добиваме една линија со една димензија - должина. Сите вектори кои опишуваат точки наоваа линија е паралелни еден на друг. Иако секоја нацртана линија има некаква дебелина (како би ја виделе), оваа идеализирана линија нема.
A Рамнината е дводимензионален објект. Има должина и широчина, но нема длабочина — како лист хартија (но и хартијата има дебелина). Претставувањето на рамнината преку вектори е малку потешко. Налинот ова да се претстави е ако земеме еден вектор и го поместиме така што така што неговата опашка се допира со главата на првиот и така обликува вектор со неговата опашка во зачетокот и главата во главата на поместениот втор вектор. Ако имаме два вектора кои не се паралелни, можеме да ги претставиме сите точки до кои ќе дојдеме со ширење на или само еден или ниеден од векторите, и, собирајќи ги сите вектори заедно, овие точки сочинуваат рамнина.
Просторот, како што го гледаме, е тридимензионален. Можеме да го претставиме како поставување на линија заедно со рамнина. Овие рамнини се „залепени заедно“ како сендвич. За да дојдеме до некоја точка во просторрот, можеме да си замислиме како патуваме нагоре низ линијата и потоа како преминуваме преку рамнината за да дојдеме до точката. Сега имаме три вектора на ум, еден за поминување на некое растојание нагоре низ линијата и два за да дојдеме до некоја точка во просторот.
Четвртата просторна димензија, иако е иста со другите три, едновремено е и тотално различна што се однесува до нашата вселена. Дека нашата вселена е составена од површина којапатува со брзина на светлината е неизбежно од Лоренцовиот трансформ кој ја дава раздалеченоста со четиридимензионален простор помеѓу два настана. Времето се множи со брзината на светлината за да се добие растојанието кое посматрачот пропатувал во надворешната димензија. Фактот дека посматрачот е на работ на вселената патувајќи со брзината на светлината, ги појаснува појавите на релативноста.
Димензионална аналогија
уредиЗа да скокнеме од три во четири димензии користиме димензионална аналогија. Димензионалната аналогија е изучувањето на соодносот помеѓу (n – 1) димензиите и n димензиите, а потоа заклучокот во каков сооднос се n димензиите со (n + 1) димензиите.
Корисна примена на димензионалната аналогија при создавање на слика за четвртата димензија е проекцијата. Проекцијата е начин на претставуање на еден n-димензионален објект во n − 1 димензии. На пример, екранот во кој гледате е дводимензионален, и сите фотографии на тридимензионални луѓе, места и нешта се претставени во две димензии со отстранување на информациите за третата димензија. Во овој случај, длабината е отсртанета и е заменета со индиректна информација. Мрежницата на окото е дводимензионален строј од рецептори, но исто така му дава на умот да ја увиди природата на тридимензионални објекти преку индиректни информации (како сенки, прелив на бои, перспектива и др). Уметниците исто така ги користат овие индиректни информации во полза на нивната уметност.
На тој начин, објектите во четвртата димензија можеме да ги проектираме математички на познатите 3 димензии, каде можеме поудобно да ги испитуваме. Во овој сучај, ,мрежницата' на четиридимензионалното око е тридимензионален строј од рецептори. Хипотетичко битие со такво око би ја увидело природата на четиридимензионалните објекти со помош на индиректните информации кои се содржат во сликите кои ги прима во неговата мрежница. Проекцијата на перспективи од четири димензии дава слични ефекти како кај оние од три, како на пример перспектива. Ова им дава четиридимензионлна длабина на овие тридимензионални слики.
Ваквата аналогија ни помага во изучувањето на проекциите. На пример, дводимензионални објекти се окружени со еднодимензионални граници: квадратот е окружен со четири линии. Тридимензионални објекти се окружени со дводимензионални површини: коцката е окружена со 6 квадрати. Со примена на димензионална аналогија, можеме да заклучиме дека четиридимензионалната коцка (хиперкоцка или тесеракт), е опкружена со тридимензионални волумени: 8 коцки. Со ова на ум, изучувањето на ваквите објекти е олеснето. Границите на хиперкоцката се проектираат во волумени во сликата, а не како дводимензионални слики.
Описот на четвртата димензија погоре нема врска со фактите за нашата вселена и затоа треба да се смета за нерелевантна на реалноста. Фактичата природа на четвртата димензија се дефинира во Лоренцовиот трансформ.
Поврзано
уреди- Векторски простор
- Евклидов простор
- Евклидова геометрија
- Многуќелијник (четиридимензионален полиедар)
- 4-многуобразие
Надворешни врски
уреди- Четвртата димензија едноставно појаснета Архивирано на 21 јануари 2003 г. (англиски)
- Гарет Џонсовата страница за тетрапростор (англиски)
- Флетленд: Романса за многу димензии Архивирано на 7 ноември 2020 г. (англиски)
- 4Д претставување Архивирано на 17 октомври 2007 г. (англиски)