Седум мостови на Кенигсберг
Седум мостови на Кенигсберг — математичка загатка и еден од позначајните историски проблеми во математиката. Отсуството на решение утврдено од страна на Леонард Ојлер во 1736 година[1] довело до поставување на основите на теоријата на графови и ја претскажала идејата за математичката гранка денес позната како топологија.[2]
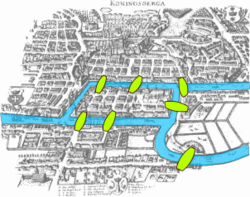
Градот Кенигсберг во Прусија (денес Калининград, Русија) бил сместен на двата брега на реката Прегел, во којашто се наоѓаат два големи острови — Кнајпхоф и Ломзе — коишто биле поврзани еден со друг или со крајбрежните делови на градот со седум мостови. Проблемот се состои во осмислување на прошетка низ градот, така што секој од мостот ќе биде преминет само еднаш. Притоа, за неприфатливо решение на проблемот се смета она коешто вклучува:
- пристигнување до остров или крајбрежен дел на градот без да се премине преку мост; или
- пристапување на било кој мост без да се премине преку неговиот друг крај.
Ојлер докажал дека проблемот нема решение. Тешкотијата со која се соочил бил развојот на соодветна техника на анализа и на последователните тестови кои го воспоставиле тврдењето со математичка строгост.
Поврзано
уредиНаводи
уреди- ↑ Euler, Leonhard (1736). "Solutio problematis ad geometriam situs pertinentis". Comment. Acad. Sci. U. Petrop 8, 128–40.
- ↑ Shields, Rob (December 2012). „Cultural Topology: The Seven Bridges of Königsburg 1736“. Theory, Culture & Society. 29 (4–5): 43–57. doi:10.1177/0263276412451161.
Надворешни врски
уреди| „Седум мостови на Кенигсберг“ на Ризницата ? |
- Ојлеровата оригинална статија (латински)
- Kaliningrad and the Konigsberg Bridge Problem на Convergence Архивирано на 8 август 2013 г.
- The Bridges of Königsberg
- How the bridges of Königsberg help to understand the brain
- Euler's Königsberg's Bridges Problem на Math Dept. Contra Costa College
- Pregel — алатка именувана по проблемот