Мрежна топологија

Мрежна топологија е план за поврзување на разновидни елементи (врски, јазли) во компјутерските мрежи. Мрежните топологии можат да бидат физички или логички. Под физичка топологија се подразбира физичкиот дизајн на мрежата вклучувајќи ги уредите, локациите и инсталацијата на каблите. Логичката топологија се однесува како податоците се пренесуваат во мрежата, спротивно на физичкиот дизајн.

Дијаграм на различни топологии

Топологијата може да се смета и како виртуелна форма на структурата на мрежата. Оваа форма не одговара на реалниот физички дизајн на уредите во компјутерската мрежа. Компјутерите во една домашна мрежа можат да бидат подредени во круг, но ова не значи дека мрежата има прстен топологија. Секоја поединечна мрежна топологија е одредена само од графичкото мапирање на конфигурацијата на физичките и/или логичките врски помеѓу јазлите. Проучувањето на мрежната топологија се темели на теоријата на графови. Растојанијата помеѓу јазлите, физичките поврзувања, ратата на пренос, и/или типовите на сигнали можат да се разликуваат во две мрежи, а сепак овие две мрежи можат да имаат идентични топологии.

Локална компјутерска мрежа (ЛАН) е еден пример за мрежа која покажува и физичка и логичка топологија. Секој даден јазол во мрежата има еден или повеќе врски со еден или повеќе јазли во истата мрежа и мапирањето на овие врски и јазли во графот резултира со геометриска форма која може да се користи за опишување на физичката топологија на мрежата. Исто така, мапирањето на протокот на податоци помеѓу јазлите во мрежата ја одредува логичката топологија на мрежата.

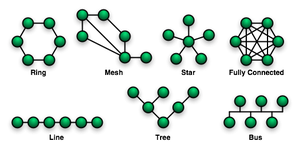
Основни видови на топологии

Постојат 7 основни топологии:

• Точка-до-точка топологија
• Магистрала
• Ѕвестеста топологија
• Топологија во вид на прстен
• Топологија во вид на дрво
• Меш топологија
• Хибридна топологија

Оваа класификација се заснова според врските помеѓу компјутерите.

Физичката топологија во мрежата се одредува од можностите на уредите за мрежен пристап и медиумите, нивото на контрола на грешки и цената на кабловите и телекомуникациските кола.

Според физичкото протегање, мрежите можат да се класифицираат како:

• Локални компјутерски мрежи (LAN)
• Мрежи во еден објект или кампус
• Широко распостранети мрежи (WAN)

Класификација на мрежните топологии

Постојат две основни категории на мрежните топологии:

• Физички топологии
• Логички топологии

Формата на распоредот на каблите кои се користат за поврзување на уредите во мрежата се нарекува физичка топологија на мрежата. Ова се однесува како каблите се поставени за да се поврзат компјутерите во една мрежа. При избор на физичка топологија, влијание имаат следните фактори:

• Распоредот на просторот
• Техники за решавање на настанати проблеми
• Цената на инсталацијата
• Типови на кабли кои се користат

Логичката топологија го опишува начинот како мрежата пренесува информација од мрежата/компјутерите до другите уреди и не зависи од физичкиот изглед на мрежата. Логичкиот изглед исто така ги опишува и различните брзини на каблите кои се користат за поврзување помеѓу мрежите.

Физички топологии

Класификација на физичките топологии

Точка-до-точка

Наједноставната топологија која претставува врска помеѓу два крајни уреди е точка-до-точка топологија. Постојат дедуцирани и преклопнички точка-до-точка топологии.

Кај дедуцираните точка-до-точка топологии, врската помеѓу двата уреди е секогаш користена, а додека пак кај преклопничките топологии, врската може да се конфигурира динамички и кога таа не се користи да биде прекината. Преклопничките точка-до-точка топологии се основниот модел кои се користат во телефонијата.

Магистрала

Топологија Магистрала

Во локалните мрежи каде се користи топологијата магистрала, секој компјутер е поврзан со еден главен кабел преку кој се пренесуваат податоците. За секој приклучен уред на главниот кабел постои конектор каде тој се приклучува. На краевите од главиот кабел постојат терминатори кои ја апсорбираат енергијата која ја носи сигналот за да не настане рефлексија и сигналот да се пренесе во обратна насока низ кабелот и на тој начин да настане интерференца. Сигналот од изворниот уред патува и во двете насоки до сите уреди приклучени на магистралата сè додека не го најде уредот со соодетна MAC и IP-адреса којшто е примач на пораката. Доколку адресата на примачот кај примениот пакет не се совпаѓа со адресата на тој уред, пакетот се отфрла. Бидејќи топологијата магистрала се состои од еден главен кабел, таа е евтина за имплементација споредено со другите топологии. Сепак, како недостатоци на овој тип топологија е цената на менаџирањето на мрежата како и доколку настане ненадејно кинење на кабелот, целата мрежа ќе падне.

Постојат линеарни и диструбуирани магистрали.

Кај линеарните магистрали, главниот кабел се состои од два краја, на кои се наоѓа по еден терминатор. Позната е под името backbone или trunk. За разлика од линеарните, дистрибуираните магистрали имаат повеќе од два краја и поголем број на терминатори. На главиот кабел постојат гранки, но за разлика од топологијата дрво, постои главен кабел – магистрала низ која се пренесуваат податоците.

Ѕвезда

Ѕвездеста топологија

Во локалните мрежи со ѕвездеста топологија, секој центар домаќин се поврзува со централно средиште (hub). За разлика од магистралата, кај ѕвездестата топологија, секој јазол се поврзува со точка-до-точка врска со централното средиште, кое носи одлука за патеката преку која ќе го прати пакетот. На тој начин, целиот сообраќај поминува низ тоа централно средиште. Ѕвездестата топологија се смета за најлесна топологија за имплементација и дизајнирање. Како предност на ѕвездестата топологија е леснотијата за додавање на дополнителен јазол во мрежата, а како недостаток доколку централното средиште престане да функционира, целата мрежа ќе падне.

Како централен уред преку којшто се поврзани уредите, не мора да биде само средиште (hub), може тоа да е и преклопник (switch), па дури и компјутер. За мрежите кои користат ѕвездеста топологија, можат да се разгледуваат и како повеќепристапни broadcast мрежи (Broadcast Multi-Access), каде централниот уред го испраќа сигналот до сите уреди приклучени на него или, пак како повеќепристапни nonbroadcast мрежи(Broadcast NonMulti-Access), каде централното средиште го испраќа сигналот до еден примач, кој смета дека е вистинскиот.

Постои и топологијата проширена ѕвезда. Кај проширените ѕвезди, компјутерите формираат подѕвезди кои сите поврзани заедно, прават топологија ѕвезда. Кај нив имаме хиерархиски подредени повеќе централни уреди, и на средината еден уред кој одлучува за сите останати.

Прстен

Топологија прстен

Топологијата во која компјутерите се поврзани во кружен облик се нарекува прстен. Секој уред во оваа топологија е поврзан со два други уреди и кога ќе прими сигнал кој не е за него, го препраќа до другиот уред. Секој уред во оваа топологија има улога на засилувач, го засилува сигналот и го праќа на другите уреди.

Како предности на ваквата топологија се: не побарува опслужувач за одржување на конективноста на мрежата, има подобри перформанси од топологијата магистрала при зголемен трансфер и е добро организирана топологија. Како недостатоци на ваквата топологија се: доколку еден уред престане да работи, настануваат проблеми во мрежата, мрежните адаптери потребни за нејзино поврзување се доста поскапи од обичните Ethernet картички.

Меш

Целосно поврзана меш топологија

Делумна поврзана меш топологија

Кај топологијата меш, секој јазол во мрежата делува како посебен насочувач, без разлика дали е поврзан со друга мрежа. Оваа топологија дозволува континуирани врски и реконфигурација откако некоја патека ќе биде блокирана или ќе престане да работи.

Топологијата во која еден јазол е директно поврзан со сите останати јазли во мрежата се нарекува целосно поврзана меш топологија. Секои два уреди се поврзани со точка-до-точка врска и бројот на овие врски во оваа мрежа изнесува n*(n-1)/2 каде n е бројот на јазли во мрежата. Како недостатоци на оваа топологија се вбројуваат скапата инсталација, тешкотијата за одржување, како и големиот број на кабли. Може да се користи доколку има мал број на компјутери во мрежата. Но како голема позитивност е тоа што доколку еден уред во мрежата престане да работи, сите останати уреди во мрежата ќе можат успешно да комуницираат.

Постои и делумна поврзана меш топологија во која не мора да постојат врски од еден јазол до сите останати. На овој начин се овозможува да се намали цената за имплементација, поголем број на компјутери кои можат да се поврзат, но пакетите не се пренесуваат директно, од тој уред до примачот, туку се испраќаат помеѓу уредите во мрежата.

Дрво

Дрво топологија

Оваа топологија е позната и како хиерархиска топологија. Дрво топологија е онаа топологија во која имаме еден уред, којшто се нарекува корен, којшто е поврзан со точка-до-точка врска со уредите од подолната хиерархија, тие на ист начин се поврзани со уредите кои се едно ниво подолу и на тој начин секој јазол си има свој родител (освен коренот) и свои наследници (деца).

За да биде топологијата дрво, мора да постојат минимум три хиерархиски нивоа. Со едно хиерархиско ниво, т.е. еден компјутер, не може да се формира мрежа, а доколку има две хиерархиски нивоа тогаш имаме ѕвездеста топологија. Бројот на врски потребни за топологијата дрво е ист со бројот на јазли одземен со 1. Бидејќи станува збор за хиерархиска топологија, на јазлите кои се наоѓаат во погорните слоеви ќе им бидат потребни повеќе процесирања за пакетот кој треба да го пратат, за разлика од јазлите кои се наоѓаат во најдолните слоеви. Факторот на гранење (број на јазли со кои е директно поврзан еден јазол) останува мал и кога бројот на јазли значително се зголемува. Затоа оваа топологија е доста корисна и високо препорачлива за имплементација.

Логички топологии

Логичката топологија, спротивно на физичката, е начинот како сигналите се однесуваат на мрежните медиуми или начинот како податоците поминуваат во мрежата од еден уред до друг не земајќи ги предвид врските помеѓу уредите. Мрежната логичка топологија не мора да биде иста како нејзината физичка топологија.

Класификација на логичките топологии

Логичката класификација на мрежните топологии генерално ги следи исите класификации како физичките топологии, патот и јазлите по кој податоците се праќаат ја определуваат топологијата. Логичките топологии се тесно поврзани со MAC методите и протоколите. Тие генерално се одредуваат од мрежните протоколи и можат да бидат динамички реконфигурирани од уреди како што се насочувачи и преклопници.

Верижно поврзани ланци (Daisy Chains)

Најлесниот начин да се додадат компјутери во мрежата е со верижно-поврзување на истите, односно крајот на едниот го поврзуваме со другиот. Доколку се праќа порака помеѓу два компјутери во ланецот од поврзани компјутери, сите опфатени компјутери ја праќаат на својот сосед и така пораката стигнува до вистинскиот примач. Постојат две форми на ваквата топологија: линеарна и прстен.

Централизација

Ѕвездестата топологија ја намалува веројатноста на паѓањето на мрежата со поврзување на периферните јазли со еден централен јазол (уред). Кога физичката логичка топологија е применета во логичка магистрална мрежа, како Етернет, централниот јазол (обично тое е средиште) ги емитува сите трансфери добиени од било кој периферен јазол до сите периферни јазли на мрежата,па понекогаш и изворниот јазол го добива емитуваниот трансфер. Сите периферни уреди исто така можат да комуницираат со сите останати јазли преку примање и праќање податоци до централниот јазол. Доколку се прекине врската помеѓу централниот јазол и еден периферен јазол, тогаш тој јазол е изолиран од останатите, но останатите јазли остануваат непроменети. Сепак, недостатокот на оваа мрежа е доколку централниот јазол престане да работи тогаш целата мрежа ќе падне.

Доколку централниот јазол е пасивен, јазолот кој сака да испрати податоци мора да толерира и ехо трансмисија, односно да ги добие назад своите податоци, чие доцнење е од дво-насочното време на пренос и доцнењето генерирано од централниот јазол. Активна ѕвездеста мрежа има активен централен јазол, кој има за задача да спречува проблеми со ехо-пораките.

Дрво топологијата (хиерархиска топологија) можа да се разгледува како колекција на ѕвездести мрежи подредени во хиерархија. Дрвото има поединечни периферни јазли (пример листови) кои пренесуваат и добиваат од другите соседни јазли и немаат улога на повторувачи или регенератори. За разлика од ѕвездестата топологија, функционалноста на централниот јазол може да биде дистрибуирана.

Како и во ѕвездестата топологија, каде некој јазол може да биде изолиран поради паѓањето на врската, истото ова може да се случи и кај хиерархиската топологија. Доколку врската кон некој лист од дрвото падне, тогаш тој лист е изолиран, а доколку станува збор за некој јазол кој не е лсит, тогаш целата секција (почнувајќи од неговите деца па до листовите) станува изолирана од останатите.

Со цел да се олесни количината на мрежен сообраќај кој доаѓа од емитувањето на сите сигнали на сите јазли, понапредни централни јазли беа развиени кои овозможуваа да се води историја на сите идентитети на сите јазли кои се поврзани во мрежата. Овие мрежни преклопници ќе „научат“ за изгледот на мрежата со „слушање“ на секоја порта при нормален трансфер на податоци, проучувајќи ги пакетите со податоци и сочувувајќи ја адресата на секој поврзан јазол и на која порта е поврзан и ќе ги складира овие податоци во својаат табела на пребарување (Lookup Table) која тој ја чува во меморијата. Оваа табела овозможува идните трансфери да бидат пратени само на планираните примачи на податоците.

Децентрализација

Во меш топологијата постојат барем два јазли кои имаат минимум две различни патеки помеѓу нив за да овозможат користење на редундантни патеки во случај доколку една од патеките падне. Ваквата децентрализација се користи како предност за компензација за паѓање на некоја врска, што претставува главниот недостаток кога се користи еден уред кој има улога на централен јазол (пример ѕвездеста и дрво топологија). Специјален тип на меш топологија, кој го ограничува бројот на скокови помеѓу два јазли е хиперкоцка (hypercube). Бројот на произволни разгранувања во меш мрежите, ги прави потешки за дизајнирање и имплементација, но нивната децентрализирачка природа ги прави многу корисни. Ова е слично на некој начин како координатна мрежа, каде линеарната или прстен топологија се користи за поврзување на системите во повеќе насоки. Како пример се повеќедимензионалните прстени, кои имаат тороидална топологија.

Целосно поврзана мрежа, целосна топологија или целосна меш топологија е мрежна топологија во која постои директна врска помеѓу сите парови на јазли. Во целосно поврзана мрежа со n јазли, постојат n(n-1)/2 директни врски. Мрежите дизајнирани со ваквата топологија често се многу скапи за инсталација, но овозможуваат висок степен на доверливост поради големиот број патишта, кои можат да се искористат за праќањето на податоците. Ваквата топологија најчесто се користи во воените апликации. Сепак, може да се забележи и кај другите протоколи за делење на заеднички ресурси, како што e BitTorrent, каде корисниците се поврзуваат во толпа. Но, во вистинската употреба на BitTorrent, секој јазол ретко кога е поврзан со сите останати јазли, како вистинска целосно поврзана мрежа, но протоколот овозможува секој јазол да биде поврзан со останатите, при делењето на заеднички ресурси.

Хибриди

Хибридните мрежи претставуваат комбинација на било кои две или повеќе топологии на таков начин што изградената мрежа не претставува стандардна топологија. Доколку поврземе две мрежи со дрво мрежа, се добива повторно мрежа со дрво топологија, но доколку поврземе две мрежи со ѕвездеста топологија, добиваме хибридна мрежна топологија. Хибридна топологија секогаш настанува која две различни основни топологии се поврзани меѓу себе. Два општи примери за хибридна мрежа се: ѕвездеста прстен мрежа и ѕвездеста мрежа магистрала.

• Ѕвездеста прстен мрежа се состои од две или повеќе ѕвездести топологии поврзани користејќи multistation access unit (MAU) како централизирано средиште
• Ѕвездеста мрежа магистрала се состои од две или повеќе ѕвездести топологии поврзани користејќи bus trunk

Додека грид мрежите станаа популарни во високоделотворните пресметковни апликации, некои системи користат генерички алгоритми за да дизајнираат свои мрежи кои имаат најмалку скокови помеѓу различните јазли. Некои од добиените распореди не се разбирливи, иако функционираат многу добро.

Снегулка топологија е навистина „Ѕвезда од ѕвезди“ мрежа, па така ги задоволува условите да стане хибридна мрежна топологија, иако не се состои од две различни основни мрежни топологии кои се поврзани заедно.

Надворешни врски

• Прирачник за мрежните топологии Архивирано на 19 септември 2008 г.
• Истражување за мрежните топологии Архивирано на 13 декември 2010 г.
• Типови на топологии Архивирано на 10 февруари 2009 г.
• Пример на логички топологии Архивирано на 6 јануари 2007 г.