Заедничка негација

Логичко нили или заедничка негација — оператор во Буловата логика кој дава резултат спротивен од логичкото или. Т.е. (не или), p НИЛИ q е точно само кога и p и q се неточни.

NOR (НИЛИ) логичка порта

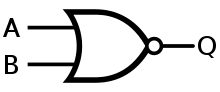
Овој оператор се нарекува и Вебова опеарација или Парсова стрелка, именувана по Чарлс Парс кој покажал дека секоја логичка операција може да се изрази по пат на НИЛИ. Така, како и НИ операторот, НИЛИ може да се користи сам, без било кој друг логички оператор, за да сочини логички формален систем (така НИЛИ е функционално потполен). Познат е и како Квајнов бодеж.

Дефиниција

НИЛИ операцијата е логичка операција на две логички вредности, особено вредностите на две тврдења кое дава вредност точно ако и само ако двата операнди се неточни. Со други зборови, дава вредност неточно ако и само ако најмалку еден операнд е точен.

Таблица на точност

Таблицата на вистинитост на p НИЛИ q (се пишува и како p ⊥ q или p ↓ q) е следнава:

p	q	↓
т	т	⊥
т	⊥	⊥
т	т	⊥
⊥	⊥	т

Венов дијаграм

Венов дијаграм за „Ниту A ниту Б“

Еден начин да се изрази p НИЛИ q е ${\overline {p\lor q}}$, каде знакот $\lor$ означува ИЛИ,а линијата над изразот означува негова негација. Најпросто $\neg (p\lor q)$. Друг начин на изразување на p НИЛИ q е ${\overline {p+q}}$.

Својства

НИЛИ нема ниеден од петте својства, од кои секое од нив треба да го нема барем во еден член на множество на функционално потполни оператори. (запазување на точност, запазување на неточност, линеарност, монотолност, самодвојност). Затоа НИЛИ само по себе е доволно за цело множество.

Заедничка негација

НИЛИ ја има интересната одлика што сите други логички оператори можат да се изразат по пат на разни функции на НИЛИ.

„не p" е еквивалентно на "p НИЛИ p“	${\overline {p}}\equiv {\overline {p+p}}$
„p и q" е еквивалентно на "(p НИЛИ p) НИЛИ (q НИЛИ q)“	$p\cdot q\equiv {\overline {{\overline {(p+p)}}+{\overline {(q+q)}}}}$
„p or q" е еквивалентно на "(p НИЛИ q) НИЛИ (p НИЛИ q)“	$p+q\equiv {\overline {{\overline {(p+q)}}+{\overline {(p+q)}}}}$
„p имплицира q" е еквивалентно на "((p НИЛИ q) НИЛИ q) НИЛИ ((p NOR q) НИЛИ q)“	$p\rightarrow q\equiv {\overline {{\overline {({\overline {(p+q)}}+q)}}+{\overline {({\overline {(p+q)}}+q)}}}}$

Логичкиот оператор НИ исто така може да ги изрази сите логички операции.

Поврзано

Амфек Битов NOR Булова алгебра Булов домен Булова функција

Функционална потполност NOR порта Исказна логика Единствен доволен оператор Логика од нулти ред