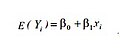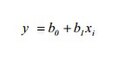Линеарен модел

Во статистиката линеарниот модел или уште се нарекува прост праволиниски регресионен модел ни ја покажува праволиниската зависност помеѓу двете појави кои ги набљудуваме. Бидејќи кај стохастичката врска меѓу двете појави се јавуваат помали или поголеми отстапувања на точките од правата, како можно решение се наметнува токму линеарниот модел кој ќе и овозможи прилагодување на правата (линија на регресија) вцртаните точки најдобро да ги репрезентира.

Равенка на правата линија: 

• 

Правата во целост е дефинираана со два коефициента:

β0 го покажува отсечокот на y-оската односно вредноста на y кога x е 0

β1 е коефициент на нагиб и го покажува тангенсот на аголот којшто ја поклопува правата со позитивен крак на x оската. Или со други зборови ја покажува промената на зависната променлива y кога независната променлива x се зголемува за една своја единица.

Ако β1 > 0 правата покажува тенденција на пораст

Акоβ1 < 0 правата покажува тенденција на опаѓање

Праволиниска функционална врска

Праволиниска функционална врска постои помеѓу пооделните вредности на xi и просечните вредности на y кои им одгогвараат на нив, а ги означуваме со E(Yi).

Регресиона линија на масата или популацијата

Регресиона линија на масата или популацијата е линијата на регресијата која минува низ просечните вредности на y за дадени вредности на xi.Таа најдобро се прилагодува на дадените податоци. Нејзината равенка гласи:

• 

Регресиона линија на примерок

Бидејќи најчесто во практиката работиме врз основа на информациите на примерокот коефициентите не можеме да ги пресметаме и затоа β0 и β1 за нас претставуваат непознати параметри исто како и аритметичката средина на масата М. Статистиката затоа за задача го има нивното оценување врз основа на податоците од примерокот и врз тие оцени би можеле да вршиме предвидување. Со изнаоѓање на таквите оцени кои ќе ги означиме со bо и b1 фактички се доаѓа до коефициентите на правата линија во примерокот . Оваа линија ја претставува регресионата линија на примерокот. Нејзината равенка гласи:

• 

Стохастички член

Стохастички член или најчесто случајна грешка претставува случајна променлива на отстапувањето на y. Стохастичкиот член е често пристутен токму затоа што вредностите на y во масата некогаш покажуваат поголемо, а некогаш помало отстапување од функционалната врска.